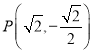题目内容
【题目】已知![]() 是函数
是函数![]() 的极值点.
的极值点.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求证:函数![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.
(参考数据:![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数)
为自然对数的底数)
【答案】(Ⅰ) ![]() (Ⅱ)见证明
(Ⅱ)见证明
【解析】
(Ⅰ)根据![]() ,求得实数
,求得实数![]() 的值,通过导数验证函数单调,可知时
的值,通过导数验证函数单调,可知时![]() 极值点为
极值点为![]() ,满足题意;
,满足题意;
(Ⅱ)由(Ⅰ) 函数![]() 的极小点值位于
的极小点值位于![]() ,此时
,此时![]() 的零点位于
的零点位于![]() ,且此
,且此![]() 为
为![]() 的极小点值点,代入
的极小点值点,代入![]() ,
,![]() 中,化简即可得到
中,化简即可得到![]() 关于
关于![]() 的二次函数,求解二次函数在区间
的二次函数,求解二次函数在区间![]() 上的值域即可证明结论。
上的值域即可证明结论。
解:(Ⅰ)因为![]() ,且
,且![]() 是极值点,
是极值点,
所以![]() ,所以
,所以![]() .
.
此时![]() ,设
,设![]() ,则
,则![]() .
.
则当![]() 时,
时,![]() 为减函数.
为减函数.
又![]() ,
,
所以在![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;![]() 时,
时,![]() ,
,![]() 为减函数.所以
为减函数.所以![]() 为
为![]() 的极大值点,符合题意.
的极大值点,符合题意.
(Ⅱ)当![]() 时,
时,![]() ,
,![]() 为增函数,且
为增函数,且![]() ,
,![]()
所以存在![]() 当
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;![]() 时,
时,![]() ,
,![]() 为增函数,所以函数
为增函数,所以函数![]() 存在唯一的极小值点
存在唯一的极小值点![]() .
.
又![]() ,已知
,已知![]() ,可得
,可得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
且满足![]() .
.
所以![]() .
.
其中![]() 也可以用如下方式证明:
也可以用如下方式证明:
![]() ,设
,设![]() ,
,
则![]() .
.
则当![]() 时,
时,![]() ,
,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
所以![]()
所以在![]() ,所以
,所以![]()

练习册系列答案
相关题目
【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: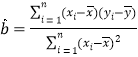
 ,
,![]() .
.