题目内容
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() .且当
.且当![]() 时,
时,![]() .若对于任意
.若对于任意![]() ,都有
,都有![]() ,则实数
,则实数![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
f(x)为周期为4的函数,且是奇函数.0在函数定义域内,故f(0)=0,得a=1,先得到[﹣1,3]一个周期内f(x)的图象,求出该周期内使f(x)≥1﹣log23成立的x的范围,从而推出![]() 的范围,再分t的范围讨论即可.
的范围,再分t的范围讨论即可.
解:由题意,f(x)为周期为4的函数,且是奇函数.0在函数定义域内,故f(0)=0,得a=1,
所以当0≤x≤1时,f(x)=log2(x+1),
当x∈[﹣1,0]时,﹣x∈[0,1],此时f(x)=﹣f(﹣x)=﹣log2(﹣x+1),
又知道f(x+2)=﹣f(x)=f(﹣x),
所以f(x)以x=1为对称轴.且当x∈[﹣1,1]时f(x)单调递增,
当x∈[1,3]时f(x)单调递减.
当x∈[﹣1,3]时,令f(x)=1﹣log23,得x![]() ,或x
,或x![]() ,
,
所以在[﹣1,3]内当f(x)>1﹣log23时,x∈[![]() ,
,![]() ].
].
设g(x)![]() ,若对于x属于[0,1]都有
,若对于x属于[0,1]都有![]() ,
,
因为g(0)![]() ∈[
∈[![]() ,
,![]() ].
].
故g(x)∈[![]() ,
,![]() ].
].
①当![]() 0时,g(x)在[0,1]上单调递减,
0时,g(x)在[0,1]上单调递减,
故g(x)∈[t![]() ,
,![]() ][
][![]() ,
,![]() ].得t≥0,无解.
].得t≥0,无解.
②0≤t≤1时,![]() ,此时g(t)最大,g(1)最小,
,此时g(t)最大,g(1)最小,
即g(x)∈[t﹣1,![]() ][
][![]() ,
,![]() ].得t∈[0,1].
].得t∈[0,1].
③当1<t≤2时,即![]() ,此时g(0)最小,g(t)最大,
,此时g(0)最小,g(t)最大,
即g(x)∈[![]() ,
,![]() ][
][![]() ,
,![]() ].得t∈(1,2],
].得t∈(1,2],
④当t>2时,g(x)在[0,1]上单调递增,
故g(x)∈[![]() ,t
,t![]() ][
][![]() ,
,![]() ].解得,t∈(2,3],
].解得,t∈(2,3],
综上t∈[0,3].
故填:[0,3].

【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: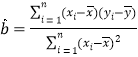
 ,
,![]() .
.
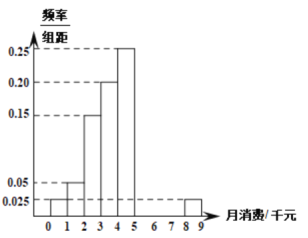
【题目】为响应低碳绿色出行,某市推出“新能源分时租赁汽车”,其中一款新能源分时租赁汽车,每次租车收费得标准由以下两部分组成:(1)根据行驶里程数按1元/公里计费;(2)当租车时间不超过40分钟时,按0.12元/分钟计费;当租车时间超过40分钟时,超出的部分按0.20元/分钟计费;(3)租车时间不足1分钟,按1分钟计算.已知张先生从家里到公司的距离为15公里,每天租用该款汽车上下班各一次,且每次租车时间t20,60(单位:分钟).由于堵车,红绿灯等因素,每次路上租车时间t是一个随即变量.现统计了他50次路上租车时间,整理后得到下表:
租车时间t(分钟) | [20,30] | (30,40] | (40,50] | (50,60] |
频数 | 2 | 18 | 20 | 10 |
将上述租车时间的频率视为概率.
(1)写出张先生一次租车费用y(元)与租车时间t(分钟)的函数关系式;
(2)公司规定,员工上下班可以免费乘坐公司接送车,若不乘坐公司接送车的每月(按22天计算)给800元车补.从经济收入的角度分析,张先生上下班应该选择公司接送车,还是租用该款新能源汽车?