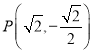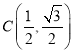题目内容
【题目】某公司代理销售某种品牌小商品，该产品进价为5元/件，销售时还需交纳品牌使用费3元/件，售价为
元/件，其中
，且
．根据市场调查，当
，且时，每月的销售量
（万件）与
成正比；当
，且
时，每月的销售量（万件）与
成反比．已知售价为15元/件时，月销售量为9万件．
（1）求该公司的月利润
（万件）与每件产品的售价（元）的函数关系式；
（2）当每件产品的售价为多少元时，该公司的月利润最大？并求出最大值．
【答案】（1）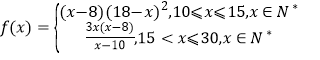
；（2）每件产品的售价为11元时，该公司的月利润
最大，且最大值为147万元.
【解析】
（1）根据h（15）＝9分别求出h（x）在不同区间上的解析式，再得出f（x）的解析式；
（2）利用导数判断f（x）的单调性，结合换元法分别求出f（x）在不同区间上的最大值，比较得出f（x）的最大值及对应的x的值．
（1）
（
，
），
，
因为当
时，
，
代入上述两式可得
，
.
所以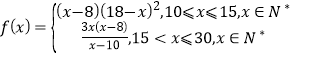
.
（2）当，时，
，
所以
，
令
，得
.
列表如下：
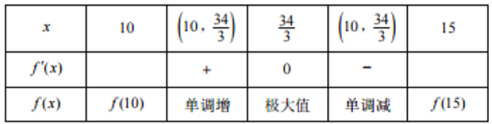
因为，且
，
，
所以当
时，
取最大值147.
当
，时，
，
令
，则
，
即
（
，
）.
因为
，所以
在且上单调递增，
所以当
时，取最大值99，此时
.
综上，当时，取最大值147.
所以当每件产品的售价为11元时，该公司的月利润最大，且最大值为147万元.
每日10分钟口算心算速算天天练系列答案
【题目】某大型超市公司计划在
市新城区开设分店，为确定在新城区开设分店的个数，该公司对该市已开设分店的其他区的数据统计后得到下列信息（其中
表示在该区开设分店的个数，
表示这个分店的年收入之和）：
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
（Ⅰ）该公司经过初步判断，可用线性回归模型拟合与的关系，求关于的回归方程；
（Ⅱ）假设该公司每年在新城区获得的总利润
（单位：万元）与，之间的关系为
，请根据（Ⅰ）中的线性回归方程，估算该公司在新城区开设多少个分店时，才能使新城区每年每个分店的平均利润最大.
参考公式：回归方程
中斜率和截距的最小二乘估计公式分别为：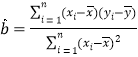
，
.
