题目内容
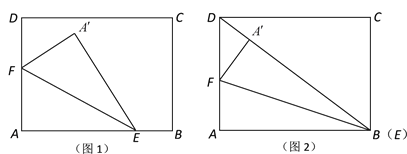
【题目】南通风筝是江苏传统手工艺品之一.现用一张长2 m,宽1.5 m的长方形牛皮纸ABCD裁剪风筝面,裁剪方法如下:分别在边AB,AD上取点E,F,将三角形AEF沿直线EF翻折到![]() 处,点
处,点![]() 落在牛皮纸上,沿
落在牛皮纸上,沿![]() ,
,![]() 裁剪并展开,得到风筝面
裁剪并展开,得到风筝面![]() ,如图1.
,如图1.
(1)若点E恰好与点B重合,且点![]() 在BD上,如图2,求风筝面
在BD上,如图2,求风筝面![]() 的面积;
的面积;
(2)当风筝面![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 到AB距离的最大值.
到AB距离的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)建立直角坐标系,求得直线![]() 的方程为
的方程为![]() ,利用点F到AB与BD的距离相等列方程可得:
,利用点F到AB与BD的距离相等列方程可得:![]() ,求得
,求得![]() ,问题得解。
,问题得解。
(2)建立直角坐标系,设![]() ,
,![]() ,
,![]() ,求得直线
,求得直线![]() 的方程为
的方程为![]() ,利用点
,利用点![]() 与
与![]() 关于直线
关于直线![]() 对称可得:
对称可得:![]() ,利用四边形
,利用四边形![]() 的面积为
的面积为![]() 可得
可得![]() ,整理得:
,整理得: ,利用导数求得
,利用导数求得![]() 的最小值为
的最小值为![]() ,即可求得
,即可求得![]() 的最大值为
的最大值为![]() ,问题得解。
,问题得解。
(1)方法一:建立如图所示的直角坐标系.
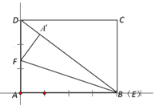
则![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() .设
.设![]() (
(![]() ),因为点F到AB与BD的距离相等,
),因为点F到AB与BD的距离相等,
所以![]() ,解得
,解得![]() 或
或![]() (舍去). 所以△ABF的面积为
(舍去). 所以△ABF的面积为![]() ,
,
所以四边形![]() 的面积为
的面积为![]() .所以风筝面
.所以风筝面![]() 的面积为
的面积为![]() .
.
方法二:设![]() ,则
,则![]() .在直角△ABD中,
.在直角△ABD中,![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() (舍去). 所以
(舍去). 所以![]() .
.
所以△ABF的面积为![]() ,所以四边形
,所以四边形![]() 的面积为
的面积为![]() .
.
所以风筝面![]() 的面积为
的面积为![]() .
.
(2)方法一:建立如图所示的直角坐标系.
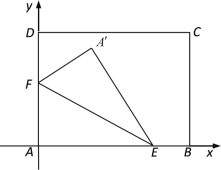
设![]() ,
,![]() ,
,![]() ,
,
则直线![]() 的方程为
的方程为![]() ,因为点A与
,因为点A与![]() 关于直线
关于直线![]() 对称,
对称,
所以 解得
解得![]() .
.
因为四边形![]() 的面积为
的面积为![]() ,所以
,所以![]() , 所以
, 所以 .
.
因为![]() ,
,![]() ,所以
,所以![]() .
.
设![]() ,
,![]() .
.![]() ,
,
令![]() ,得
,得![]() 或
或![]() (舍去).列表如下:
(舍去).列表如下:
|
|
| |
|
| 0 |
|
| 单调递减 | 极小值 | 单调递增 |
当![]() 时,
时,![]() 取得极小值,即最小值
取得极小值,即最小值![]() ,
,
所以![]() 的最大值为
的最大值为![]() ,所以点
,所以点![]() 到AB距离的最大值为
到AB距离的最大值为![]() 。
。
方法二:设![]() ,
,![]() ,则
,则![]() .因为四边形
.因为四边形![]() 的面积为
的面积为![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() .过点
.过点![]() 作AB的垂线
作AB的垂线![]() ,垂足为T,
,垂足为T,
则![]()
 .
.
因为![]() ,
,![]() ,所以
,所以![]() .
.

(下同方法一)

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: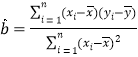
 ,
,![]() .
.
【题目】为响应低碳绿色出行,某市推出“新能源分时租赁汽车”,其中一款新能源分时租赁汽车,每次租车收费得标准由以下两部分组成:(1)根据行驶里程数按1元/公里计费;(2)当租车时间不超过40分钟时,按0.12元/分钟计费;当租车时间超过40分钟时,超出的部分按0.20元/分钟计费;(3)租车时间不足1分钟,按1分钟计算.已知张先生从家里到公司的距离为15公里,每天租用该款汽车上下班各一次,且每次租车时间t20,60(单位:分钟).由于堵车,红绿灯等因素,每次路上租车时间t是一个随即变量.现统计了他50次路上租车时间,整理后得到下表:
租车时间t(分钟) | [20,30] | (30,40] | (40,50] | (50,60] |
频数 | 2 | 18 | 20 | 10 |
将上述租车时间的频率视为概率.
(1)写出张先生一次租车费用y(元)与租车时间t(分钟)的函数关系式;
(2)公司规定,员工上下班可以免费乘坐公司接送车,若不乘坐公司接送车的每月(按22天计算)给800元车补.从经济收入的角度分析,张先生上下班应该选择公司接送车,还是租用该款新能源汽车?