题目内容
【题目】随着生活水平的提高,人们的休闲方式也发生了变化.某机构随机调查了![]() 个人,其中男性占调查人数的
个人,其中男性占调查人数的![]() .已知男性中有一半的人的休闲方式是运动,而女性只有
.已知男性中有一半的人的休闲方式是运动,而女性只有![]() 人的休闲方式是运动.
人的休闲方式是运动.
(1)完成下列![]() 列联表:
列联表:
运动 | 非运动 | 总计 | |
男性 | |||
女性 | |||
总计 | n |
(2)若在犯错误的概率不超过![]() 的前提下,可认为“性别与休闲方式有关”, 那么本次被调查的人数至少有多少?
的前提下,可认为“性别与休闲方式有关”, 那么本次被调查的人数至少有多少?
(3)根据(2)的结论,本次被调查的人中,至少有多少人的休闲方式是运动?
参考公式![]() ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)
运动 | 非运动 | 总计 | |
|
|
|
|
|
|
|
|
|
|
|
|
(2)140;(3)56.
【解析】
试题(1)依据某机构随机调查了n个人,其中男性占调查人数的![]() .已知男性中有一半的人的休闲方式是运动,而女性只有
.已知男性中有一半的人的休闲方式是运动,而女性只有![]() 的人的休闲方式是运动.即可完成表格;(2)将表格中的数据代入
的人的休闲方式是运动.即可完成表格;(2)将表格中的数据代入![]() ,得到
,得到![]() ,解出
,解出![]() 即可;(3)由(2)知,
即可;(3)由(2)知,![]() 即为所求.
即为所求.
(1)依意:被调查的男性人数为![]() ,其中有
,其中有![]() 人的休闲方式是运动;被调查的女性人数为
人的休闲方式是运动;被调查的女性人数为![]() ,其中有
,其中有![]() 人的休闲方式是运动,则
人的休闲方式是运动,则![]() 列联表如下:
列联表如下:
运动 | 非运动 | 总计 | |
|
|
|
|
|
|
|
|
|
|
|
|
(2) 由表中数据,得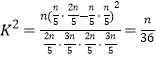 .
.
要在犯错误的概率不超过0.05的前提下,认为“性别与休闲方式有关”,
则![]() ,
,
所以![]() ,解得
,解得![]() . 又
. 又![]() ,且
,且![]() ,∴
,∴![]() .
.
故本次被调查的人数至少是140人.
(3) 由(2)可知![]() ,
,
所以,本次被调查的人中至少有56人的休闲方式是运动.

【题目】某大型超市公司计划在![]() 市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中
市新城区开设分店,为确定在新城区开设分店的个数,该公司对该市已开设分店的其他区的数据统计后得到下列信息(其中![]() 表示在该区开设分店的个数,
表示在该区开设分店的个数,![]() 表示这
表示这![]() 个分店的年收入之和):
个分店的年收入之和):
分店个数 | 2 | 3 | 4 | 5 | 6 |
年收入 | 250 | 300 | 400 | 450 | 600 |
(Ⅰ)该公司经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)假设该公司每年在新城区获得的总利润![]() (单位:万元)与
(单位:万元)与![]() ,
,![]() 之间的关系为
之间的关系为![]() ,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
,请根据(Ⅰ)中的线性回归方程,估算该公司在新城区开设多少个分店时,才能使新城区每年每个分店的平均利润最大.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: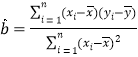
 ,
,![]() .
.