题目内容
8.设函数f(x)=lnx-$\frac{1}{2}a{x^2}+x({a>-\frac{1}{4}})$.(Ⅰ)若函数f(x)在点(1,f(1))处的切线与直线y=x平行,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)当a=0,m>0时,方程2mf(x)=x2有唯一实数解,求m的值.
分析 (Ⅰ)求出函数的导数,求得切线的斜率,结合直线平行的条件,解方程可得a;
(Ⅱ)求出导数,对a讨论,当a=0时,当-$\frac{1}{4}$<a<0时,当a>0时,由导数的符号,确定函数的单调性;
(Ⅲ)研究函数是单调性得到函数的极值点,根据函数图象的变化趋势,判断何时方程2mf(x)=x2有唯一实数解,得到m所满足的方程,解方程求解m.
解答 解:(Ⅰ)函数f(x)=lnx-$\frac{1}{2}a{x^2}+x({a>-\frac{1}{4}})$的导数为f′(x)=$\frac{1}{x}$-ax+1,
f(x)在点(1,f(1))处的切线斜率为1-a+1=2-a,
由切线与直线y=x平行,可得2-a=1,解得a=1;
(Ⅱ)当a=0时,f′(x)=$\frac{x+1}{x}$>0,即有f(x)在(0,+∞)递增;
当-$\frac{1}{4}$<a<0时,f′(x)=$\frac{-a{x}^{2}+x+1}{x}$(x>0)>0恒成立,
即有f(x)在(0,+∞)递增;
当a>0时,1+4a>0,设-ax2+x+1=0的两根为x1=$\frac{1+\sqrt{1+4a}}{2a}$>0,x2=$\frac{1-\sqrt{1+4a}}{2a}$<0,
f′(x)>0解得x2<x<x1,由x>0,则0<x<x1,
f′(x)<0解得x>x1,或x<x2,由x>0,则x>x1.
综上可得,当-$\frac{1}{4}$<a≤0时,f(x)在(0,+∞)递增;
当a>0时,f(x)在(0,$\frac{1+\sqrt{1+4a}}{2a}$)上递增,在($\frac{1+\sqrt{1+4a}}{2a}$,+∞)递减;
(Ⅲ)因为方程2mf(x)=x2有唯一实数解,
所以x2-2mlnx-2mx=0有唯一实数解,
设g(x)=x2-2mlnx-2mx,
则g′(x)=$\frac{2{x}^{2}-2mx-2m}{x}$,令g′(x)=0,x2-mx-m=0.
因为m>0,x>0,所以x1=$\frac{m-\sqrt{{m}^{2}+4m}}{2}$<0(舍去),x2=$\frac{m+\sqrt{{m}^{2}+4m}}{2}$,
当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上单调递减,
当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)单调递增,
当x=x2时,g(x)取最小值g(x2).
则$\left\{\begin{array}{l}{g({x}_{2})=0}\\{g′({x}_{2})=0}\end{array}\right.$,即$\left\{\begin{array}{l}{{{x}_{2}}^{2}-2mln{x}_{2}-2m{x}_{2}=0}\\{{{x}_{2}}^{2}-m{x}_{2}-m=0}\end{array}\right.$,
所以2mlnx2+mx2-m=0,因为m>0,所以2lnx2+x2-1=0(*),
设函数h(x)=2lnx+x-1,因为当x>0时,h(x)是增函数,
所以h(x)=0至多有一解.
因为h(1)=0,所以方程(*)的解为x2=1,即$\frac{m+\sqrt{{m}^{2}+4m}}{2}$=1,
解得m=$\frac{1}{2}$.
点评 本题考查导数的运用:求切线的斜率和单调区间以及极值、最值,同时考查分类讨论的思想方法和函数方程的思想,考查运算能力,属于中档题.

 应用题作业本系列答案
应用题作业本系列答案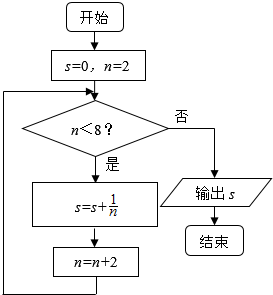 如图所示,程序框图的输出结果是( )
如图所示,程序框图的输出结果是( )| A. | $\frac{1}{16}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{3}{4}$ |
 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.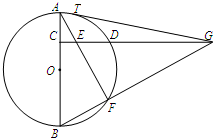 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T. 将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上. 如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.
如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.