题目内容
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?
【答案】
(1)解:作散点图如图所示.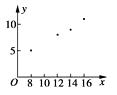
(2)解:由散点图可知y与x线性相关,故可设回归直线方程为 ![]() =bx+a.
=bx+a.
可算得, ![]() =12.5,
=12.5, ![]() =8.25,
=8.25, ![]() ,
, ![]() ,
,
∴ ![]() ,a=
,a= ![]() -b
-b ![]() ≈8.25-0.73×12.5=-0.875.
≈8.25-0.73×12.5=-0.875.
∴所求回归直线方程为 ![]() =0.73x-0.875
=0.73x-0.875
(3)解:令 ![]() =10,得0.73x-0.875=10,解得x≈15.
=10,得0.73x-0.875=10,解得x≈15.
即机器的运转速度应控制在15转/秒内
【解析】(1)根据题目给出的数据可以作出散点图。
(2)由散点图可知y与x线性相关,通过设回归直线方程,由回归直线方程计算公式可以求出方程。
(3)通过令![]() =10,将其代入方程,可以解出x的值。
=10,将其代入方程,可以解出x的值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校在校学生2 000人,为了学生的“德、智、体”全面发展,学校举行了跑步和登山比赛活动,每人都参加而且只参与其中一项比赛,各年级参与比赛的人数情况如下表:
高一年级 | 高二年级 | 高三年级 | |
跑步人数 | a | b | c |
登山人数 | x | y | z |
其中a∶b∶c=2∶5∶3,全校参与登山的人数占总人数的 ![]() .为了了解学生对本次活动的满意程度,从中抽取一个200人的样本进行调查,则高三年级参与跑步的学生中应抽取( )
.为了了解学生对本次活动的满意程度,从中抽取一个200人的样本进行调查,则高三年级参与跑步的学生中应抽取( )
A.15人
B.30人
C.40人
D.45人