题目内容
【题目】已知f(x)是R上的奇函数,且当x>0时,f(x)=-2x2+4x+3.
(1)求f(x)的表达式;
(2)画出f(x)的图象,并指出f(x)的单调区间.
【答案】
(1)解:设x<0,则-x>0,
于是f(-x)=-2(-x)2-4x+3=-2x2-4x+3.
又∵f(x)为奇函数,∴f(-x)=-f(x).
因此f(x)=2x2+4x-3.
又∵f(0)=0,
∴f(x)= 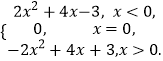
(2)解:先画出y=f(x)(x>0)的图象,利用奇函数的对称性可得到相应y=f(x)(x<0)的图象,其图象如图所示.由图可知,其增区间为[-1,0)和(0,1],减区间为(-∞,-1]和[1,+∞).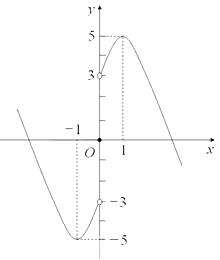
【解析】(1)由奇函数在y轴一偶的解析式,由对称性可求出在y轴另一偶的解析式;
(2)函数是分段函数,作出图象,由图象观察得到单调区间.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?