题目内容
【题目】已知函数![]()
(1)若当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(2)设![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
【答案】(1) ![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)解法一:求得函数导数并通分,对![]() 分成
分成![]() 两种情况,结合函数的单调性、最值,求得实数
两种情况,结合函数的单调性、最值,求得实数![]() 的取值范围.解法二:将原不等式
的取值范围.解法二:将原不等式![]() 分离常数
分离常数![]() ,得到
,得到![]() ,构造函数
,构造函数![]() ,利用导数结合洛必达法则,求得
,利用导数结合洛必达法则,求得![]() 的取值范围,由此求得
的取值范围,由此求得![]() 的取值范围.(2)解法一:先由(1)的结论,证得当
的取值范围.(2)解法一:先由(1)的结论,证得当![]() 时
时![]() 成立.再利用导数证得当
成立.再利用导数证得当![]() 时,
时,![]() 也成立,由此证得不等式成立.解法二:将所要证明的不等式等价转化为
也成立,由此证得不等式成立.解法二:将所要证明的不等式等价转化为![]() ,构造函数
,构造函数![]() ,利用导数证得
,利用导数证得![]() ,进而证得
,进而证得![]() ,也即证得
,也即证得![]() .
.
解:(1)【解法一】由![]() 得:
得:
![]()
①当![]() 时,由
时,由![]() 知,
知,![]()
![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]() 当
当![]() 时,
时,![]() 恒成立,
恒成立,
所以当![]() 时,满足题意;
时,满足题意;
②当![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数.
上是增函数.
这时当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]()
即![]() 在
在![]() 上为减函数,所以
上为减函数,所以![]()
即![]() 在
在![]() 上的最小值
上的最小值![]() ,
,
此时,当![]() 时,
时,![]() 不可能恒成立,即有
不可能恒成立,即有![]() 不满足题意.
不满足题意.
综上可知,当![]() ,使
,使![]() 恒成立时,
恒成立时,
![]() 的取值范围是
的取值范围是![]() .
.
【解法二】
当![]() 时,
时,![]() 等价于
等价于![]()
令![]() ,则只须使
,则只须使![]()
![]()
设![]()
![]() 在
在![]() 上为增函数,
上为增函数,![]()
所以![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]()
由洛必达法则知![]()
即当![]() 时,
时,![]() ,所以有
,所以有![]()
即当![]() ,使
,使![]() 恒成立时,则
恒成立时,则![]() 的取值范围是
的取值范围是![]()
(2)解法一:由(1)知,当![]() 时,
时,
当![]() 时,
时,![]()
又![]()
![]()
![]() 成立
成立
故只须在证明,当![]() 时,
时,![]() 即可
即可
当![]() 时,
时,![]()
又当![]() 时,
时,![]()
![]()
所以,只须证明![]() 即可;
即可;
设![]()
由![]() 得:
得:![]()
![]() 当
当![]() ,时
,时![]()
当![]() 时,
时,![]()
即![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数,
上为减函数,
![]() 当
当![]() 时,
时,![]()
![]() 成立
成立
综上可知,当![]() 时,
时,![]() 成立.
成立.
(2)解法二:由(1)知当![]() 时,
时,![]()
等价于![]()
设![]()
由![]() 得:
得:![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
即![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数,
上为减函数,
![]() 当
当![]() 时,
时,
![]()
因为![]() 时,
时,![]() .所以
.所以![]()
所以![]() 成立.
成立.
综上可知,当![]() 时,
时,![]() 成立.
成立.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到0.1).
精确到0.1).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为
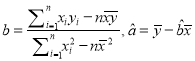 ,相关系数
,相关系数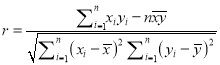
参考数据:
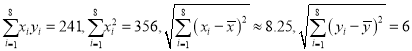 .
.



