题目内容
【题目】甲、乙、丙3人均以游戏的方式决定是否参加学校音乐社团、美术社团,游戏规则为:
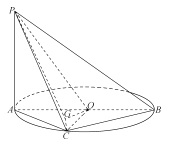
①先将一个圆8等分(如图),再将8个等分点![]() ,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心
,分别标注在8个相同的小球上,并将这8个小球放入一个不透明的盒子里,每个人从盒内随机摸出两个小球、然后用摸出的两个小球上标注的分点与圆心![]() 构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
构造三角形.若能构成直角三角形,则两个社团都参加;若能构成锐角三角形,则只参加美术社团;若能构成钝角三角形,则只参加音乐社团;若不能构成三角形,则两个社团都不参加.
②前一个同学摸出两个小球记录下结果后,把两个小球都放回盒内,下一位同学再从盒中随机摸取两个小球。

(1)求甲能参加音乐社团的概率;
(2)记甲、乙、丙3人能参加音乐社团的人数为随机变量![]() ,求
,求![]() 的分布列、数学期望和方差
的分布列、数学期望和方差
【答案】(1) ![]() ;(2)分布列见解析; 数学期望
;(2)分布列见解析; 数学期望![]() ;方差
;方差![]()
【解析】
(1)先求得基本事件的总数为![]() ,然后计算出与圆心
,然后计算出与圆心![]() 构成直角三角形或钝角三角形的取法数之和,再利用古典概型概率计算公式,求得所求概率.(2)利用二项分布概率计算公式,计算出分布列,并求得数学期望和方差.
构成直角三角形或钝角三角形的取法数之和,再利用古典概型概率计算公式,求得所求概率.(2)利用二项分布概率计算公式,计算出分布列,并求得数学期望和方差.
解:(1)从盒中随机摸出两个小球,即是从8个等分点中随机选取两个不同的分点,共有![]() 种,其中与圆心
种,其中与圆心![]() 构成直角三角形的取法有8种:
构成直角三角形的取法有8种:![]() ,与圆心
,与圆心![]() 构成钝角三角形的取法有
构成钝角三角形的取法有![]() 种:
种: ![]() .所以甲能参加音乐社团的概率为:
.所以甲能参加音乐社团的概率为:![]() .
.
(2)由题意可知:![]() ,
,![]() 的可能取值为:0,1,2,3.
的可能取值为:0,1,2,3.
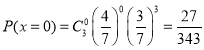
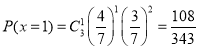
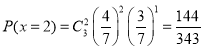
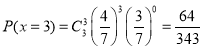
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望![]()
方差![]()

【题目】下表为2015年至2018年某百货零售企业的年销售额![]() (单位:万元)与年份代码
(单位:万元)与年份代码![]() 的对应关系,其中年份代码
的对应关系,其中年份代码![]() 年份-2014(如:
年份-2014(如:![]() 代表年份为2015年)。
代表年份为2015年)。
年份代码 | 1 | 2 | 3 | 4 |
年销售额 | 105 | 155 | 240 | 300 |
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测2019年该百货零售企业的年销售额;
的线性回归方程,并预测2019年该百货零售企业的年销售额;
(2)2019年,美国为遏制我国的发展,又祭出“长臂管辖”的霸权行径,单方面发起对我国的贸易战,有不少人对我国经济发展前景表示担忧.此背景下,某调查平台为了解顾客对该百货零售企业的销售额能否持续增长的看法,随机调查了60为男顾客、50位女顾客,得到如下![]() 列联表:
列联表:
持乐观态度 | 持不乐观态度 | 总计 | |
男顾客 | 45 | 15 | 60 |
女顾客 | 30 | 20 | 50 |
总计 | 75 | 35 | 110 |
问:能否在犯错误的概率不超过0.05的前提下认为对该百货零售企业的年销售额持续增长所持的态度与性别有关?
参考公式及数据:回归直线方程 ,
,
![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.