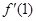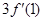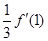题目内容
是否存在实数a,使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数?如果存在,求出a的取值范围;如果不存在,请说明理由.
见解析
解:假设符合条件的实数a存在,
设g(x)=ax2-x,
当a>1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,需g(x)=ax2-x在区间[2,4]上是增函数,故应满足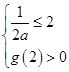
即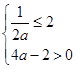 解得a>
解得a>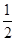 .
.
又∵a>1,∴a>1;
当0<a<1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,需g(x)=ax2-x在区间[2,4]上是减函数,故应满足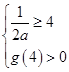 即
即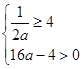
此不等式组无解;
综上可知:当a>1时,函数f(x)=loga(ax2-x)在区间[2,4]上是增函数.
设g(x)=ax2-x,
当a>1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,需g(x)=ax2-x在区间[2,4]上是增函数,故应满足
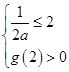
即
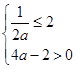 解得a>
解得a>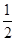 .
.又∵a>1,∴a>1;
当0<a<1时,为使函数f(x)=loga(ax2-x)在区间[2,4]上是增函数,需g(x)=ax2-x在区间[2,4]上是减函数,故应满足
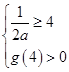 即
即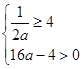
此不等式组无解;
综上可知:当a>1时,函数f(x)=loga(ax2-x)在区间[2,4]上是增函数.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
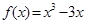 ,过点P
,过点P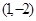 的直线
的直线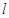 与曲线
与曲线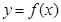 相切,求
相切,求 ,当
,当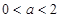 时,
时,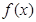 在1,4上的最小值为
在1,4上的最小值为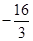 ,求
,求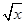 ,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )
,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )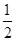
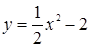 上一点P(1,
上一点P(1,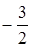 ),则过点P的切线的倾斜角为( )
),则过点P的切线的倾斜角为( )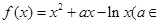
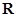 ).
).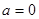 时,求函数
时,求函数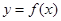 在点
在点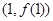 处的切线方程;
处的切线方程;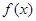 在
在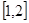 上是减函数,求实数
上是减函数,求实数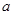 的取值范围;
的取值范围;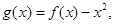 是否存在实数
是否存在实数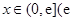 是自然对数的底)时,函数
是自然对数的底)时,函数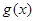 的最小值是
的最小值是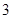 .若存在,求出
.若存在,求出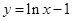 在
在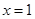 处的切线方程为 .
处的切线方程为 .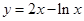 在点
在点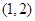 处的切线方程是 .
处的切线方程是 .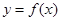 在
在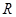 上可导,则
上可导,则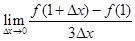 等于( )
等于( )