题目内容
已知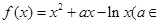
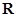 ).
).
(1)若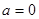 时,求函数
时,求函数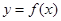 在点
在点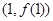 处的切线方程;
处的切线方程;
(2)若函数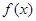 在
在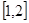 上是减函数,求实数
上是减函数,求实数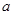 的取值范围;
的取值范围;
(3)令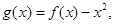 是否存在实数
是否存在实数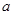 ,当
,当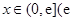 是自然对数的底)时,函数
是自然对数的底)时,函数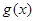 的最小值是
的最小值是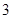 .若存在,求出
.若存在,求出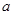 的值;若不存在,说明理由.
的值;若不存在,说明理由.
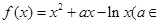
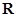 ).
).(1)若
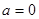 时,求函数
时,求函数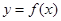 在点
在点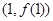 处的切线方程;
处的切线方程;(2)若函数
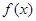 在
在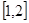 上是减函数,求实数
上是减函数,求实数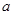 的取值范围;
的取值范围;(3)令
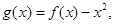 是否存在实数
是否存在实数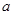 ,当
,当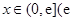 是自然对数的底)时,函数
是自然对数的底)时,函数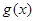 的最小值是
的最小值是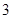 .若存在,求出
.若存在,求出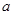 的值;若不存在,说明理由.
的值;若不存在,说明理由.(1)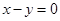 ;(2)
;(2)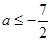 ;(3)存在实数
;(3)存在实数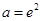 ,使
,使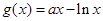 在
在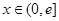 上的最小值是
上的最小值是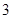 .
.
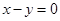 ;(2)
;(2)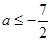 ;(3)存在实数
;(3)存在实数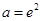 ,使
,使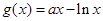 在
在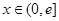 上的最小值是
上的最小值是 .
.试题分析:(1)当
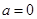 时,
时,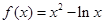 ,求其在切点处的导函数值,得到切线斜率,由点斜式即得所求;
,求其在切点处的导函数值,得到切线斜率,由点斜式即得所求;(2)函数
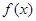 在
在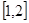 上是减函数,转化成
上是减函数,转化成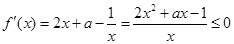 在
在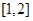 上恒成立;
上恒成立;令
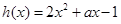 ,解
,解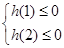 即得
即得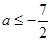 ;
;(3)假设存在实数
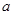 ,使
,使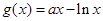 在
在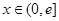 上的最小值是
上的最小值是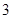 ,根据
,根据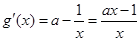 ,
,讨论当
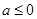 、
、 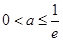 、
、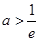 等三种情况时,令
等三种情况时,令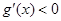 ,求解即得.
,求解即得.(1)当
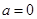 时,
时,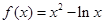
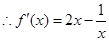 1分
1分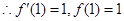 ,函数
,函数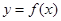 在点
在点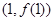 处的切线方程为
处的切线方程为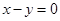 3分
3分(2)函数
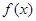 在
在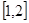 上是减函数
上是减函数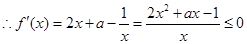 在
在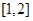 上恒成立 4分
上恒成立 4分令
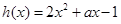 ,有
,有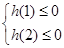 得
得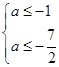 6分
6分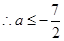 7分
7分 (3)假设存在实数
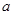 ,使
,使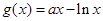 在
在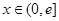 上的最小值是3
上的最小值是3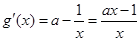 8分
8分当
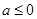 时,
时,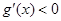 ,
,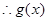 在
在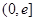 上单调递减,
上单调递减,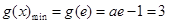
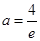 (舍去) 10分
(舍去) 10分当
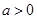 且
且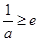 时,即
时,即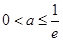 ,
,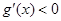 在
在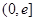 上恒成立,
上恒成立,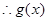 在
在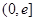 上单调递减
上单调递减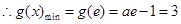 ,
,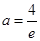 (舍去) 11分
(舍去) 11分当
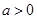 且
且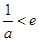 时,即
时,即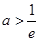 时,令
时,令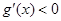 ,得
,得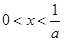 ;
;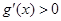 ,得
,得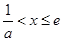
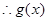 在
在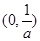 上单调递减,在
上单调递减,在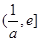 上单调递增
上单调递增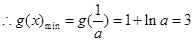 ,
,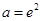 满足条件 13分
满足条件 13分综上所述,存在实数
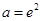 ,使
,使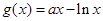 在
在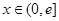 上的最小值是
上的最小值是 . 14分
. 14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
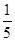 x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.
x2的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=________.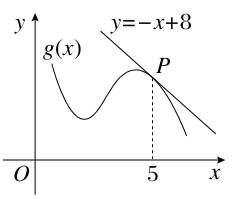
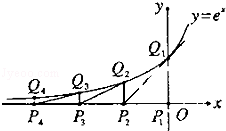
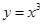 在
在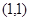 处的切线与
处的切线与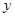 轴交点的纵坐标为( )
轴交点的纵坐标为( )
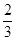
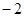
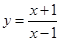 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线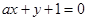 垂直,则
垂直,则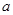 的值是
的值是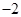
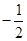
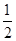
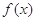 =1+
=1+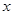 +
+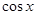 在
在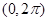 上是( )
上是( )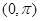 上增,在
上增,在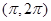 上减
上减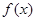 的导函数为
的导函数为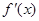 ,且满足关系式
,且满足关系式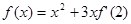 ,则
,则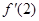 的值等于( )
的值等于( )