题目内容
6.(1)函数f(x)=(1+$\sqrt{3}$tanx)cosx的最小正周期;(2)求f(x)的单调增区间;
(3)求f(x)的最大值和最小值.
分析 (1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(x+$\frac{π}{6}$),由三角函数的周期性及其求法即可得解.
(2)由2kπ$-\frac{π}{2}$≤x+$\frac{π}{6}$≤2k$π+\frac{π}{2}$,k∈Z可解得f(x)的单调增区间.
(3)由正弦函数的图象和性质可得sin(x+$\frac{π}{6}$)∈[-1,1],从而可求f(x)的最大值和最小值.
解答 解:(1)∵f(x)=(1+$\sqrt{3}$tanx)cosx
=cosx+$\sqrt{3}$sinx
=2sin(x+$\frac{π}{6}$),
∴最小正周期T=$\frac{2π}{1}$=2π.
(2)由2kπ$-\frac{π}{2}$≤x+$\frac{π}{6}$≤2k$π+\frac{π}{2}$,k∈Z可解得f(x)的单调增区间为:[2k$π-\frac{2π}{3}$,2k$π+\frac{π}{3}$](k∈Z).
(3)∵sin(x+$\frac{π}{6}$)∈[-1,1],
∴f(x)=2sin(x+$\frac{π}{6}$)∈[-2,2],即f(x)的最大值为2,最小值为-2.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
16.若a<b<0,则( )
| A. | a2c>b2c(c∈R) | B. | $\frac{b}{a}>1$ | C. | lg(a-b)>0 | D. | ${({\frac{1}{2}})^a}>{({\frac{1}{2}})^b}$ |
17.定义复数的一种运算z1*z2=$\frac{|{z}_{1}|+|{z}_{2}|}{2}$ (等式右边为普通运算),若复数z=a+bi,$\overline{z}$为z的共轭复数,且正实数a,b满足a+b=3,则z*$\overline{z}$的最小值为( )
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
11.关于函数y=4x2+$\frac{1}{x}$在x∈(0,+∞)上的最值的说法,下列正确的是( )
| A. | 最大值为3,无最小值 | B. | 无最大值,最小值为3 | ||
| C. | 无最大值,无最小值 | D. | 无最大值,最小值为$\frac{33}{2}$ |
15.设0<b<a<1,则下列不等式不成立的是( )
| A. | 2b<2a<2 | B. | $0<{log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}$b | ||
| C. | ab<b2<1 | D. | ab<a2<1 |
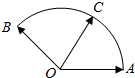 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.