题目内容
16．若a＜b＜0，则（ ）| A． | a2c＞b2c（c∈R） | B． | $\frac{b}{a}＞1$ | C． | lg（a-b）＞0 | D． | ${（{\frac{1}{2}}）^a}＞{（{\frac{1}{2}}）^b}$ |
分析 根据不等式的基本性质，指数函数的单调性和对数函数的真数范围，逐一分析四个答案的真假，可得答案．
解答 解：若a＜b＜0，则a2＞b2，但当c≤0时，a2c＞b2c不成立，故A错误；
若a＜b＜0，则$0＜\frac{b}{a}＜1$，故B错误；
若a＜b＜0，则a-b＜0，lg（a-b）无意义，故C错误；
若a＜b＜0，则${（\frac{1}{2}）}^{a}＞{（\frac{1}{2}）}^{b}$，故D正确；
故选：D．
点评 本题考查的知识点是不等式的基本性质，指数函数的单调性和对数函数的真数范围，难度不大，属于基础题．
练习册系列答案
相关题目
11．与直线x-y+4=0和圆x2+y2-2x+2y=0都相切的半径最小的圆的方程是（ ）
| A． | （x+1）2+（y+1）2=2 | B． | （x+1）2+（y-1）2=2 | C． | （x+1）2+（y+1）2=4 | D． | （x+1）2+（y-1）2=4 |
8．
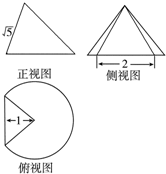一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的表面积为（ ）
一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的表面积为（ ）| A． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B． | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |