题目内容

11．关于函数y=4x2+$\frac{1}{x}$在x∈（0，+∞）上的最值的说法，下列正确的是（　　）
A．最大值为3，无最小值B．无最大值，最小值为3
C．无最大值，无最小值D．无最大值，最小值为$\frac{33}{2}$

分析 x∈（0，+∞），f（x）=4x2+$\frac{1}{x}$，利用导数研究其单调性极值与最值即可得出．

解答 解：∵x∈（0，+∞），f（x）=4x2+$\frac{1}{x}$，
∴f′（x）=8x-$\frac{1}{{x}^{2}}$=$\frac{8{x}^{3}-1}{{x}^{2}}$=$\frac{（2x-1）（4{x}^{2}+2x+1）}{{x}^{2}}$，由f′（x）=0，解得x=$\frac{1}{2}$．
当x$＞\frac{1}{2}$时，f′（x）＞0，函数f（x）单调递增；当$0＜x＜\frac{1}{2}$时，f′（x）＜0，函数f（x）单调递减．
∴当x=$\frac{1}{2}$时，函数f（x）取得最小值，$f（\frac{1}{2}）$=3．
而当x→+∞或x→0+时，f（x）→+∞，
因此函数f（x）有最小值3，而无最大值．
故选：B．

点评 本题考查了利用导数研究其单调性极值与最值的方法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
1．设互不相等的正整数a1，a2，…，an（n≥2，n∈N+）组成的集合为M={ a1，a2，…，an}，定义集合S={（a，b）|a∈M，b∈M，a-b∈M}．
（1）若M={1，2，3，4}，则集合S中的元素最多有6个．
（2）若M={ a1，a2，…，an}，则集合S是的元素最多有$\frac{1}{2}$n（n-1） 个．
2．若$\frac{π}{2}$＜α＜π，化简$\sqrt{\frac{1+sinα}{1-sinα}}-\sqrt{\frac{1-sinα}{1+sinα}}$的结果是（　　）
A．-2tanαB．2tanαC．-2cotαD．2cotα
19．已知离散型随机变量ξ的概率分布如表格：
ξ135
P0.5m0.2
则其数学期望E（ξ）等于（　　）
A．1B．0.6C．2+3mD．2.4
6．（1）函数f（x）=（1+$\sqrt{3}$tanx）cosx的最小正周期；
（2）求f（x）的单调增区间；
（3）求f（x）的最大值和最小值．
16．（Ⅰ）若等差数列{an}满足：a1=20，an=54，前n项和Sn=999，求公差d及项数n；
（Ⅱ）若等比数列{an}满足：a1=-1，a4=64，求公比q及前n项和Sn．
3．已知等差数列{an}的首项a1=1，公差d＞0，前n项和Sn
（1）若S1，S2，S4成等比数列，求数列$\left\{{\frac{a_n}{2^n}}\right\}$的前n项和Tn；
（2）若$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$＞$\frac{2015}{2016}$对一切n∈N*恒成立，求d的取值范围．
20．设x，y满足约束条件$\left\{\begin{array}{l}x+y≥3\\ x-y≥-1\\ 2x-y≤3\end{array}\right.$，若目标函数z=abx+y（a＞0，b＞0）的最大值为8，则a+b的最小值为$\sqrt{3}$．
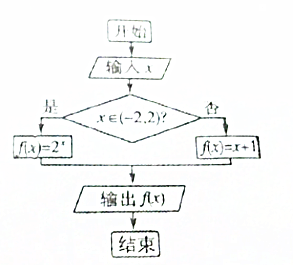1．阅读如图的程序框图，若输出的函数值f（x）为4，则输入的自变量x的值为3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网