题目内容
4.已知$\overrightarrow{OA}$=(2,1),$\overrightarrow{OB}$=(1,7),$\overrightarrow{OC}$=(5,1),若$\overrightarrow{OD}$=x•$\overrightarrow{OA}$,y=$\overrightarrow{DB}$•$\overrightarrow{DC}$(x、y∈R).(1)求y=f(x)的解析式;
(2)求y=f(x)的图象按向量$\overrightarrow{a}$=(-2,8)平移后得到的图象y=g(x)的解析式;
(3)过原点O作OM、ON分别交于y=g(x)的图象于M、N两点,直线MN交y轴于点Q(0,y0),当∠MON为锐角时,求y0的取值范围.
分析 (1)根据向量数量积的坐标公式即可求y=f(x)的解析式;
(2)根据向量平移关系即可求出y=g(x)的解析式;
(3)设M(m,5m2),N(n,5n2),根据∠MON为锐角时,建立不等式关系进行求解即可.
解答 解:(1)∵$\overrightarrow{OD}$=x•$\overrightarrow{OA}$=(2x,x),∴D(2x,x),
∵$\overrightarrow{OB}$=(1,7),$\overrightarrow{OC}$=(5,1),
∴B=(1,7),C(5,1),
∴$\overrightarrow{DB}$=(1-2x,7-x),$\overrightarrow{DC}$=(5-2x,1-x),
则y=$\overrightarrow{DB}$•$\overrightarrow{DC}$=(1-2x,7-x)•(5-2x,1-x)=5x2-20x+12,
即y=f(x)=5x2-20x+12;
(2)∵y=f(x)=5x2-20x+12=5(x-2)2-8,
∴y=f(x)的图象按向量$\overrightarrow{a}$=(-2,8)平移后得到的图象y=g(x)=5x2;
(3)设M(m,5m2),N(n,5n2),
则直线MN的方程为$\frac{y-5{n}^{2}}{5{m}^{2}-5{n}^{2}}=\frac{x-n}{m-n}$,
令x=0,则y0=-5mn,
若∠MON为锐角,则$\overrightarrow{OM}•\overrightarrow{ON}$=mn+25m2n2>0,
∴mn$<-\frac{1}{25}$或mn>0
即y0<0或y0>$\frac{1}{5}$,
故y0的取值范围是(-∞,0)∪($\frac{1}{5}$,+∞).
点评 本题主要考查向量的数量积公式的应用,以及向量平移的关系,考查学生的运算能力.

| A. | -$\frac{{\sqrt{5}}}{5}$ | B. | -$\frac{2}{5}\sqrt{5}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{2}{5}\sqrt{5}$ |
(1-x)10g(x)+h(x),则a9=( )
| A. | 0 | B. | 10×219 | C. | -10×218 | D. | -3×218 |
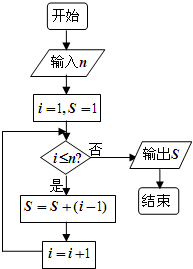
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
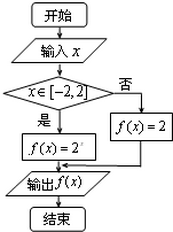 阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )
阅读程序框图,如果输出的函数值在区间[2,4]内,则输入的实数x的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2) | C. | [1,+∞) | D. | (-∞,-2)∪[1,+∞) |

| A. |  | B. |  | C. |  | D. |  |