题目内容

15．已知g（x）=a0+a1x+a2x2+…+a10x10，h（x）=b0+b1x+b2x2+…+b9x9，若（1+x）（1-2x）19 =
（1-x）10g（x）+h（x），则a9=（　　）
A．0B．10×219C．-10×218D．-3×218

分析 根据等式（1+x）（1-2x）19 =（1-x）10g（x）+h（x）的两边展开式中的x19的系数相等、x20的系数相等求得a9的值．

解答 解：由（1+x）（1-2x）19 =（1-x）10g（x）+h（x）=（1-x）10•（a0+a1x+a2x2+…+a10x10）+b0+b1x+b2x2+…+b9x9 ，
可得x19的系数相等可得 ${C}_{19}^{19}$•（-2）19+${C}_{19}^{18}$•（-2）18=${C}_{10}^{10}$•a9-${C}_{10}^{9}$•a10 ①，
再根据x20的系数相等可得 ${C}_{19}^{19}$•（-2）19=${C}_{10}^{10}$a10 ②．
由①②求得 a9=-3×218，
故选：D．

点评 本题考查了二项式定理的运用；关键是通过系数的关系找到与所求有关的等式，属于中档题．

练习册系列答案
相关题目
5．在△ABC中，已知sinA=2sinB•cosC，且（a+b+c）（b+c-a）=3bc，则△ABC为（　　）
A．等边三角形B．钝角三角形C．直角三角形D．等腰直角三角形
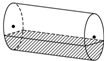6．已知f1（x）=sinx，fn（x）=f′n-1（x），n≥2，则$\sum_{i=1}^{2008}{{f_i}（0）=}$0．
3．${（2x-\frac{1}{2}）^6}$展开式中x2的系数为$\frac{15}{4}$．
10．一个水平放置的圆柱形储油桶（如图所示），桶内有油部分所在圆弧占底面圆周长的$\frac{1}{4}$，则油桶直立时，油的高度与桶的高度的比值是$\frac{1}{4}$-$\frac{1}{2π}$．（结果保留π）
20．已知函数f（x）=（x-a）2+（x-b）2+（x-c）2+$\frac{（a+b+c）^{2}}{3}$（a，b，c为实数）
①求f（x）的最小值m（用a，b，c表示）；
②若a-b+2c=3，求（1）中m的最小值．
7．已知P是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$上的一个动点，F1，F2分别是左右焦点，则cos∠F1PF2的最小值为$-\frac{1}{9}$．
4．已知$\overrightarrow{OA}$=（2，1），$\overrightarrow{OB}$=（1，7），$\overrightarrow{OC}$=（5，1），若$\overrightarrow{OD}$=x•$\overrightarrow{OA}$，y=$\overrightarrow{DB}$•$\overrightarrow{DC}$（x、y∈R）．
（1）求y=f（x）的解析式；
（2）求y=f（x）的图象按向量$\overrightarrow{a}$=（-2，8）平移后得到的图象y=g（x）的解析式；
（3）过原点O作OM、ON分别交于y=g（x）的图象于M、N两点，直线MN交y轴于点Q（0，y0），当∠MON为锐角时，求y0的取值范围．
5．函数y=log${\;}_{\frac{1}{2}}$sin（$\frac{π}{4}$-$\frac{x}{2}$）的单调递增区间是[4kπ-$\frac{π}{2}$，4kπ+$\frac{π}{2}$），k∈Z．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网