题目内容

5．能够把圆O：x2+y2=16的周长和面积同时分为相等的两部分的函数称为圆O的“和谐函数”，下列函数不是圆O的“和谐函数”的是（　　）
A．f（x）=4x3+xB．f（x）=ex+e-xC．f（x）=tan$\frac{x}{2}$D．f（x）=ln$\frac{5-x}{5+x}$

分析 由“和谐函数”的定义及选项知，该函数若为“和谐函数”，其函数须为过原点的奇函数，由此逐项判断即可得到答案

解答 解：若函数f（x）是圆O的“和谐函数”，则函数的图象经过圆心且关于圆心对称，
由圆O：x2+y2=16的圆心为坐标原点，故函数f（x）是奇函数，
由于A中f（x）=x+4x3，C中f（x）=tan$\frac{x}{2}$，D中f（x）=1n$\frac{5-x}{5+x}$都为奇函数，而f（x）=ex+e-x为偶函数，不满足要求．
故选B

点评 本题考查的知识点是函数的奇偶性，其中根据新定义圆O的“和谐函数”判断出满足条件的函数为奇函数是解答的关键．

练习册系列答案
相关题目
15．设函数f（x）=ex+ax+b在点（0，f（0））处的切线方程为x+y+1=0．
（Ⅰ）求a，b值，并求f（x）的单调区间；
（Ⅱ）证明：当x≥0时，f（x）＞x2-4．
16．已知（$\frac{1}{2}$-ix）10=a0+a1x+a2x2+…+a10x10（i为虚数单位），则a0+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{4}$+…+$\frac{{a}_{10}}{{2}^{10}}$=$-\frac{i}{32}$．
13．点P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上一点，F是右焦点，且△OPF是∠POF=120°的等腰三角形（O为坐标原点），则双曲线的离心率是$\sqrt{3}$+1．
20．已知向量$\overrightarrow{a}$=（$\sqrt{3}$sin2x，sinx+cosx），$\overrightarrow{b}$=（1，sinx-cosx），其中x∈R，记函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$．
（1）求f（x）的最小正周期；
（2）若f（$\frac{θ}{2}$）=$\frac{\sqrt{3}}{2}$，且$\frac{2π}{3}$＜θ＜$\frac{7π}{6}$，求cosθ的值．
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{\sqrt{3}}{2}$），离心率为$\frac{\sqrt{3}}{2}$．
（1）求椭圆C的方程；
（2）不垂直与坐标轴的直线l与椭圆C交于A，B两点，线段AB的垂直平分线交y轴于点P（0，$\frac{1}{3}$），若cos∠APB=-$\frac{1}{3}$，求直线l的方程．
17．如图是一个几何体的三视图，则该几何体可能是（　　）
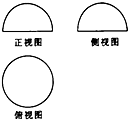
A．半球B．球C．圆柱D．圆锥
14．若二项式（x3+$\frac{1}{x}$）n的展开式中含有x8的项，则正整n的最小值为4•
15．偶函数f（x）=loga|x+b|在（-∞，0）上单调递减，则f（a+1）与f（2-b）的大小关系是（　　）
A．f（a+1）＞f（2-b）B．f（a+1）=f（2-b）C．f（a+1）＜f（2-b）D．不能确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网