题目内容
15.设函数f(x)=ex+ax+b在点(0,f(0))处的切线方程为x+y+1=0.(Ⅰ)求a,b值,并求f(x)的单调区间;
(Ⅱ)证明:当x≥0时,f(x)>x2-4.
分析 (Ⅰ)求函数的导数,利用导数的几何意义以及切线方程建立方程关系即可求a,b值以及f(x)的单调区间;
(Ⅱ)构造函数,利用导数研究函数的单调性和最值关系即可证明不等式.
解答 解:(Ⅰ)f′(x)=ex+a,
由已知,f′(0)=-1,f(0)=-1,
故a=-2,b=-2,
f′(x)=ex-2,
当x∈(-∞,ln2)时,f′(x)<0,当x∈(ln2,+∞)时,f′(x)>0,
故f(x)在(-∞,ln2)单调递减,在(ln2,+∞)单调递增;…(6分)
(Ⅱ)设g(x)=f(x)-(x2-4)=ex-x2-2x+2,
g′(x)=ex-2x-2=f(x)在(ln2,+∞)单调递增,在(-∞,ln2)单调递减,
因为g′(0)=-1<0,g′(2)=e2-6>0,0<ln2<2,
所以g′(x)在[0,+∞)只有一个零点x0,且x0∈(0,2),${e}^{{x}_{0}}$=2x0+2,
当x∈[0,x0)时,g′(x)<0,
当x∈(x0,+∞)时,g′(x)>0,
即g(x)在[0,x0)调递减,在(x0,+∞)时,单调递增,
当x≥0时,g(x)≥g(x0)=${e}^{{x}_{0}}-{{x}_{0}}^{2}-2{x}_{0}+2$=4-${{x}_{0}}^{2}$>0,
即f(x)>x2-4,…(12分)
点评 本题主要考查导数的几何意义以及函数单调性的应用,综合考查导数的应用,运算量较大,综合性较强.

练习册系列答案
相关题目
3.设函数$f(x)=\left\{{\begin{array}{l}{ln(-x){,_{\;}}x<0}\\{-lnx,{{,}_{\;}}x>0}\end{array}}\right.$若f(m)>f(-m),则实数m的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | .(-∞,-1)∪(0,1) | C. | (-1,0)∪(1,+∞) | D. | (-1,1] |
4.在△ABC中,角A,B,C的对边分别是a,b,c,若a2-b2=$\sqrt{3}$bc,sinC=2$\sqrt{3}$sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
5.能够把圆O:x2+y2=16的周长和面积同时分为相等的两部分的函数称为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A. | f(x)=4x3+x | B. | f(x)=ex+e-x | C. | f(x)=tan$\frac{x}{2}$ | D. | f(x)=ln$\frac{5-x}{5+x}$ |
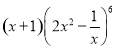 的展开式的常数项为_________________.
的展开式的常数项为_________________.