题目内容
16.已知($\frac{1}{2}$-ix)10=a0+a1x+a2x2+…+a10x10(i为虚数单位),则a0+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{4}$+…+$\frac{{a}_{10}}{{2}^{10}}$=$-\frac{i}{32}$.分析 利用赋值法,以及二项式定理的简单性质,求解即可.
解答 解:($\frac{1}{2}$-ix)10=a0+a1x+a2x2+…+a10x10(i为虚数单位),
令x=$\frac{1}{2}$,可得($\frac{1}{2}$-$\frac{1}{2}$i)10=a0+$\frac{1}{2}$a1+$\frac{1}{4}$a2+…+$\frac{1}{{2}^{10}}$a10(i为虚数单位),
而($\frac{1}{2}$-$\frac{1}{2}$i)10=$\frac{{[(1-i)}^{2}]^{5}}{{2}^{10}}$=$\frac{{[-2i]}^{5}}{{2}^{10}}$=$-\frac{i}{32}$.
故答案为:$-\frac{i}{32}$.
点评 本题考查二项式定理的应用,赋值法的应用,考查计算能力.

练习册系列答案
相关题目
4.在△ABC中,角A,B,C的对边分别是a,b,c,若a2-b2=$\sqrt{3}$bc,sinC=2$\sqrt{3}$sinB,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
8.已知a,b是空间中两不同直线,α,β是空间中两不同平面,下列命题中正确的是( )
| A. | 若直线a∥b,b?α,则a∥α | B. | 若平面α⊥β,a⊥α,则a∥β | ||
| C. | 若平面α∥β,a?α,b?β,则a∥b | D. | 若a⊥α,b⊥β,a∥b,则α∥β |
5.能够把圆O:x2+y2=16的周长和面积同时分为相等的两部分的函数称为圆O的“和谐函数”,下列函数不是圆O的“和谐函数”的是( )
| A. | f(x)=4x3+x | B. | f(x)=ex+e-x | C. | f(x)=tan$\frac{x}{2}$ | D. | f(x)=ln$\frac{5-x}{5+x}$ |
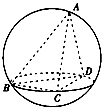 如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD是全等的等腰三角形,且平面ACD⊥平面BCD,AB=2CD=4,则该三棱锥的外接球的表面积为$\frac{65}{4}π$.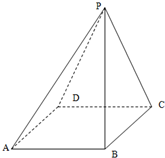 如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.
如图:四棱锥P-ABCD中,底面ABCD是边长为2的正方形,平面PCD⊥底面ABCD,且PC=PD=a.