题目内容
15．偶函数f（x）=loga|x+b|在（-∞，0）上单调递减，则f（a+1）与f（2-b）的大小关系是（ ）| A． | f（a+1）＞f（2-b） | B． | f（a+1）=f（2-b） | C． | f（a+1）＜f（2-b） | D． | 不能确定 |
分析 由条件利用函数的奇偶性的性质、函数的单调性的性质，判断函数的奇偶性和单调性．
解答 解：根据函数f（x）=loga|x+b|为偶函数，可得f（-x）=fx），即loga|-x+b|=loga|x+b|，b=0，故f（x）=loga|x|．
再根据f（x）=loga|x|在（-∞，0）上单调递减，可得a＞1，∴（a+1）＞2-b=2．
由偶函数的性质可得f（x）=loga|x|在（0，+∞）上单调递增，∴f（a+1）＞f（2-b），
故选：A．
点评 本题主要考查函数的奇偶性和单调性的综合应用，属于基础题．
练习册系列答案
相关题目
5．能够把圆O：x2+y2=16的周长和面积同时分为相等的两部分的函数称为圆O的“和谐函数”，下列函数不是圆O的“和谐函数”的是（ ）
| A． | f（x）=4x3+x | B． | f（x）=ex+e-x | C． | f（x）=tan$\frac{x}{2}$ | D． | f（x）=ln$\frac{5-x}{5+x}$ |
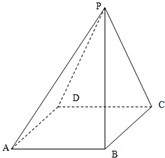如图：四棱锥P-ABCD中，底面ABCD是边长为2的正方形，平面PCD⊥底面ABCD，且PC=PD=a．