题目内容
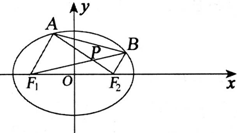
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(1,$\frac{\sqrt{3}}{2}$),离心率为$\frac{\sqrt{3}}{2}$.(1)求椭圆C的方程;
(2)不垂直与坐标轴的直线l与椭圆C交于A,B两点,线段AB的垂直平分线交y轴于点P(0,$\frac{1}{3}$),若cos∠APB=-$\frac{1}{3}$,求直线l的方程.
分析 (Ⅰ)运用椭圆的离心率公式和点满足方程及a,b,c的关系,即可得到椭圆方程;
(Ⅱ)设直线l的方程设为y=kx+t,设A(x1,y1)B(x2,y2),联立椭圆方程,运用韦达定理和判别式大于0,以AB为直径的圆过坐标原点,求出中点坐标,再由点到直线距离公式和弦长公式代入化简整理,再由两直线垂直的条件,解方程可得k,进而得到所求直线方程.
解答 解:(Ⅰ)由题意得$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,且$\frac{1}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,又a2-b2=c2,
解得a=2,b=1.
所以椭圆C的方程是$\frac{{x}^{2}}{4}$+y2=1.
(Ⅱ)设直线l的方程设为y=kx+t,设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+t}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$消去y得(1+4k2)x2+8ktx+4t2-4=0,
则有x1+x2=$\frac{-8kt}{1+4{k}^{2}}$,x1x2=$\frac{4{t}^{2}-4}{1+4{k}^{2}}$,
由△>0可得1+4k2>t2,
y1+y2=kx1+t+kx2+t=k(x1+x2)+2t=$\frac{2t}{1+4{k}^{2}}$
设A,B的中点为D(m,n),则m=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{4kt}{1+4{k}^{2}}$,n=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{t}{1+4{k}^{2}}$
因为直线PD与直线l垂直,所以kPD=-$\frac{1}{k}$=$\frac{\frac{1}{3}-n}{-m}$,得$\frac{t}{1+4{k}^{2}}$=-$\frac{1}{9}$,
△>0可得4k2+1>t2,可得-9<t<0,
因为cos∠APB=2cos2∠APD-1=-$\frac{1}{3}$,
所以cos∠APD=$\frac{\sqrt{3}}{3}$,可得tan∠APD=$\sqrt{2}$,
所以$\frac{\frac{|AB|}{2}}{|PD|}$=$\sqrt{2}$,由点到直线距离公式和弦长公式可得|PD|=$\frac{|-\frac{1}{3}+t|}{\sqrt{1+{k}^{2}}}$,
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{(\frac{-8kt}{1+4{k}^{2}})^{2}-\frac{16{t}^{2}-16}{1+4{k}^{2}}}$=$\frac{4\sqrt{(1+{k}^{2})(1+4{k}^{2}-{t}^{2})}}{1+4{k}^{2}}$,
由$\frac{\frac{|AB|}{2}}{|PD|}$=$\frac{\frac{2\sqrt{(1+{k}^{2})(1+4{k}^{2}-{t}^{2})}}{1+4{k}^{2}}}{\frac{|-\frac{1}{3}+t|}{\sqrt{1+{k}^{2}}}}$=$\sqrt{2}$和$\frac{t}{1+4{k}^{2}}$=-$\frac{1}{9}$,
解得t=-1∈(-9,0),k=$±\sqrt{2}$,
直线l的方程为y=$\sqrt{2}$x-1或y=-$\sqrt{2}$x-1.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率的运用和方程的运用,联立直线方程,运用韦达定理,弦长公式,同时考查圆的性质:直径所对的圆周角为直角,考查直线垂直的条件和直线方程的求法,属于难题.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | f(x)=4x3+x | B. | f(x)=ex+e-x | C. | f(x)=tan$\frac{x}{2}$ | D. | f(x)=ln$\frac{5-x}{5+x}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |