题目内容
9．已知集合M={x|$\sqrt{x+1}$≥0}，集合N={x|x2+x-2＜0}，则M∩N=[-1，1）．分析 求出M中x的范围确定出M，求出N中不等式的解集确定出N，找出两集合的交集即可．
解答 解：由M中$\sqrt{x+1}$≥0，得到x+1≥0，即x≥-1，
∴M=[-1，+∞），
由N中不等式变形得：（x-1）（x+2）＜0，
解得：-2＜x＜1，即N=（-2，1），
则M∩N=[-1，1）；
故答案为：[-1，1）
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
20．
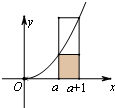如图所示，由直线x=a，x=a+1（a＞0），y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间，即a2＜${∫}_{a}^{a+1}$x2dx＜（a+1）2．类比之，?n∈N*，$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$＜A＜$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立，则实数A等于（ ）
如图所示，由直线x=a，x=a+1（a＞0），y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间，即a2＜${∫}_{a}^{a+1}$x2dx＜（a+1）2．类比之，?n∈N*，$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$＜A＜$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立，则实数A等于（ ）| A． | $\frac{1}{2}$ | B． | $\frac{3}{5}$ | C． | ln2 | D． | ln$\frac{5}{2}$ |
4．已知sinx+$\sqrt{3}$cosx=$\frac{8}{5}$，则cos（$\frac{π}{6}$-x）=（ ）
| A． | -$\frac{3}{5}$ | B． | $\frac{3}{5}$ | C． | -$\frac{4}{5}$ | D． | $\frac{4}{5}$ |
14．下列说法正确的是（ ）
| A． | 命题“若x=y，则sinx=siny”的否命题为真命题 | |
| B． | “直线x-ay=0与直线x+ay=0互相垂直”的充分条件是“a=1” | |
| C． | 命题“?x∈R，x2+x+1＜0”的否定是“?x∈R，x2+x+1＞0” | |
| D． | 命题：若x2=1，则x=1或x=-1的逆否命题为：若x≠1或x≠-1，则x2≠1 |
1．已知 m、n 是两条不重合的直线，α、β、γ是三个互不重合的平面，则下列命题中 正确的是（ ）
| A． | 若 m∥α，n∥α，则 m∥n | B． | 若α⊥γ，β⊥γ，则 α∥β | ||
| C． | 若m⊥α，n⊥α，则 m∥n | D． | 若 m∥α，m∥β，则 α∥β |
18．已知集合A={-2，a}，B={2a，b}，若A∩B={1}，则A∪B=（ ）
| A． | {-2，1，3} | B． | {-2，1，2} | C． | {-2，1} | D． | {-2，1，5} |