题目内容
设曲线y=x2+x+1-ln x在x=1处的切线为l,数列{an}中,a1=1,且点(an,an+1)在切线l上.
(1)求证:数列{1+an}是等比数列,并求an;
(2)求数列{an}的前n项和Sn.
(1)求证:数列{1+an}是等比数列,并求an;
(2)求数列{an}的前n项和Sn.
(1)由y=x2+x+1-ln x,知x=1时,y=3.
又y′|x=1=2x+1-|x=1=2,
∴切线l的方程为y-3=2(x-1),即y=2x+1.
∵点(an,an+1)在切线l上,
∴an+1=2an+1,1+an+1=2(1+an).
又a1=1,∴数列{1+an}是首项为2,公比为2的等比数列,
∴1+an=2·2n-1,即an=2n-1(n∈N*).
(2)Sn=a1+a2+…+an=(21-1)+(22-1)+…+(2n-1)
=2+22+…+2n-n=2n+1-2-n.
又y′|x=1=2x+1-|x=1=2,
∴切线l的方程为y-3=2(x-1),即y=2x+1.
∵点(an,an+1)在切线l上,
∴an+1=2an+1,1+an+1=2(1+an).
又a1=1,∴数列{1+an}是首项为2,公比为2的等比数列,
∴1+an=2·2n-1,即an=2n-1(n∈N*).
(2)Sn=a1+a2+…+an=(21-1)+(22-1)+…+(2n-1)
=2+22+…+2n-n=2n+1-2-n.
略

练习册系列答案
相关题目
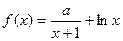 (
(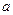 为实常数)的两个极
为实常数)的两个极 值点为
值点为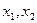 ,且满足
,且满足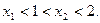
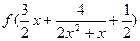 与
与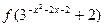 的大小.
的大小.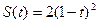 的直线运动,则其在
的直线运动,则其在 时的瞬时速度为:
时的瞬时速度为: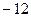
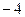
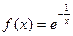 ,则
,则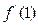 = ___________.
= ___________.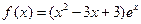
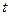 的取值范围,使得函数
的取值范围,使得函数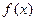 在
在 上为单调函数;
上为单调函数; 时,判断
时,判断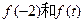 的大小,并说明理由;
的大小,并说明理由;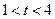 时,关于
时,关于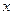 的方程
的方程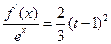 在区间
在区间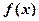 是定义在实数集
是定义在实数集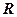 上的不恒为零的偶函数,
上的不恒为零的偶函数,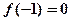 ,且对任意实数
,且对任意实数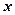 都
都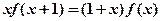 ,则
,则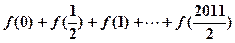 的值是
的值是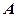 .
.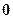

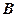 .
. 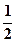
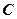 .
. 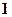
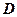 .
.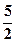
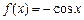 ,
,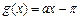 .
.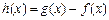 在
在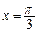 时取得极值,求
时取得极值,求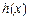 的单调递减区间;
的单调递减区间;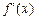 |≤| x |;
|≤| x |;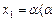 ∈[
∈[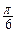 ,
,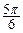 ]),
]),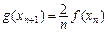 ,求证:
,求证: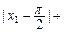
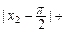 …+
…+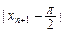 <
<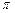 (n∈N*).
(n∈N*).