题目内容
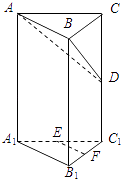
【题目】如图1,在![]() 中,
中, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
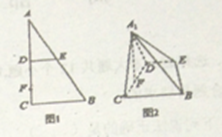
(1)求证: ![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.
【答案】(1)见解析(2)线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.
【解析】试题分析:(1)由题意可证DE⊥平面A1DC,从而有DE⊥A1F,又A1F⊥CD,可证A1F⊥平面BCDE,问题解决;
(2)取A1C,A1B的中点P,Q,则PQ∥BC,平面DEQ即为平面DEP,由DE⊥平面,P是等腰三角形DA1C底边A1C的中点,可证A1C⊥平面DEP,从而A1C⊥平面DEQ.
试题解析:
(1)证明:由已知得![]() 且
且![]() ,
,
![]() ,又
,又![]() ,
, ![]() 平面
平面![]() ,面
,面![]() 平面
平面![]() ,
,
![]() ,
,
又![]() 平面
平面![]() ,
,
![]() .
.
(2)线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.
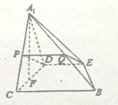
理由如下:如图,分别取![]() 的中点
的中点![]() ,则
,则![]() .
.
![]() 平面
平面![]() 即为平面
即为平面![]() .
.
由(1)知![]() 平面
平面![]() ,
,
又![]() 是等腰三角形
是等腰三角形![]() 底边
底边![]() 的中点
的中点![]() ,
,
![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]() ,
,
故线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.

练习册系列答案
相关题目
【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应关系:
x/百万元 | 2 | 4 | 5 | 6 | 8 |
y/百万元 | 30 | 40 | 60 | 50 | 70 |
(1)假定y与x之间有线性相关关系,求其回归直线方程;
(2)若实际的销售额不少于60百万元,则广告费支出应不少于多少?