ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ –ΉΦ±Η‘ΎΒά¬Ζ![]() ΒΡ“Μ≤ύ–όΫ®“ΜΧθ‘ΥΕ·±»»ϋΒάΘ§»ϋΒάΒΡ«Α“Μ≤ΩΖ÷ΈΣ«ζœΏΕΈ
ΒΡ“Μ≤ύ–όΫ®“ΜΧθ‘ΥΕ·±»»ϋΒάΘ§»ϋΒάΒΡ«Α“Μ≤ΩΖ÷ΈΣ«ζœΏΕΈ![]() Θ§ΗΟ«ζœΏΕΈ «Κ· ΐ
Θ§ΗΟ«ζœΏΕΈ «Κ· ΐ![]() Θ§
Θ§ ![]() ±ΒΡΆΦœσΘ§«“ΆΦœσΒΡΉνΗΏΒψΈΣ
±ΒΡΆΦœσΘ§«“ΆΦœσΒΡΉνΗΏΒψΈΣ![]() .»ϋΒάΒΡ÷–Φδ≤ΩΖ÷ΈΣ≥Λ
.»ϋΒάΒΡ÷–Φδ≤ΩΖ÷ΈΣ≥Λ![]() «ßΟΉΒΡ÷±œΏ≈ήΒά
«ßΟΉΒΡ÷±œΏ≈ήΒά![]() Θ§«“
Θ§«“![]() .»ϋΒάΒΡΚσ“Μ≤ΩΖ÷ «“‘
.»ϋΒάΒΡΚσ“Μ≤ΩΖ÷ «“‘![]() ΈΣ‘≤–ΡΒΡ“ΜΕΈ‘≤ΜΓ
ΈΣ‘≤–ΡΒΡ“ΜΕΈ‘≤ΜΓ![]() .
.
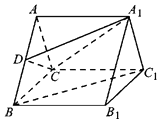
(1)«σ![]() ΒΡ÷ΒΚΆ
ΒΡ÷ΒΚΆ![]() ΒΡ¥σ–ΓΘΜ
ΒΡ¥σ–ΓΘΜ
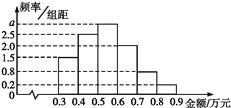
(2)»τ“Σ‘Ύ‘≤ΜΓ»ϋΒάΥυΕ‘”ΠΒΡ…»–Έ![]() «χ”ρΡΎΫ®“ΜΗωΓΑΨΊ–Έ≤ίΤΚΓ±Θ§ΨΊ–ΈΒΡ“Μ±Ώ‘ΎΒά¬Ζ
«χ”ρΡΎΫ®“ΜΗωΓΑΨΊ–Έ≤ίΤΚΓ±Θ§ΨΊ–ΈΒΡ“Μ±Ώ‘ΎΒά¬Ζ![]() …œΘ§“ΜΗωΕΞΒψ‘ΎΑκΨΕ
…œΘ§“ΜΗωΕΞΒψ‘ΎΑκΨΕ![]() …œΘ§ΝμΆβ“ΜΗωΕΞΒψ
…œΘ§ΝμΆβ“ΜΗωΕΞΒψ![]() ‘Ύ‘≤ΜΓ
‘Ύ‘≤ΜΓ![]() …œΘ§«“
…œΘ§«“![]() ,«σΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐ»ΓΉν¥σ÷Β ±
,«σΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐ»ΓΉν¥σ÷Β ±![]() ΒΡ÷Β.
ΒΡ÷Β.
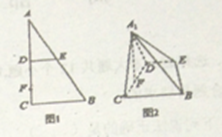
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§ ![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() .
.
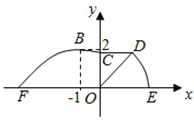
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
Θ®1Θ©”…Χβ“βΩ…ΒΟ![]() Θ§Ι
Θ§Ι ![]() Θ§¥”ΕχΩ…ΒΟ«ζœΏΕΈ
Θ§¥”ΕχΩ…ΒΟ«ζœΏΕΈ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§Ννx=0Ω…ΒΟ
Θ§Ννx=0Ω…ΒΟ![]() Θ§ΗυΨί
Θ§ΗυΨί![]() Θ§ΒΟ
Θ§ΒΟ![]() ,“ρ¥Υ
,“ρ¥Υ![]() Θ®2Θ©ΫαΚœΧβ“βΩ…ΒΟΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΉν¥σ ±Θ§Βψ
Θ®2Θ©ΫαΚœΧβ“βΩ…ΒΟΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΉν¥σ ±Θ§Βψ![]() ‘ΎΜΓ
‘ΎΜΓ![]() …œΘ§”…ΧθΦΰΩ…ΒΟΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ
…œΘ§”…ΧθΦΰΩ…ΒΟΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ![]() Θ§»ΜΚσΗυΨί
Θ§»ΜΚσΗυΨί![]() ΒΡΖΕΈßΩ…ΒΟΒ±
ΒΡΖΕΈßΩ…ΒΟΒ±![]() ±Θ§
±Θ§![]() »ΓΒΟΉν¥σ÷ΒΘ°
»ΓΒΟΉν¥σ÷ΒΘ°
‘ΧβΫβΈωΘΚ
(1)”…ΧθΦΰΒΟ![]() .
.
Γύ![]() .
.
Γύ«ζœΏΕΈ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() .
.
Β±![]() ±Θ§
±Θ§![]() .
.
”÷![]() Θ§
Θ§
Γύ![]() ,
,
Γύ![]() .
.
(2)”…(1)Θ§Ω…÷Σ![]() .
.
”÷“Ή÷ΣΒ±ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΉν¥σ ±Θ§Βψ![]() ‘ΎΜΓ
‘ΎΜΓ![]() …œΘ§Ι
…œΘ§Ι ![]() .
.
…η![]() ,
,![]() ,ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ
,ΓΑΨΊ–Έ≤ίΤΚΓ±ΒΡΟφΜΐΈΣ
![]()
![]() .
.
ΓΏ![]() Θ§
Θ§
Γύ![]() ,
,
Ι Β±![]() Θ§Φ¥
Θ§Φ¥![]() ±Θ§
±Θ§![]() »ΓΒΟΉν¥σ÷ΒΘ°
»ΓΒΟΉν¥σ÷ΒΘ°

 ΤΎΡ©Ϋπ≈ΤΨμœΒΝ–¥πΑΗ
ΤΎΡ©Ϋπ≈ΤΨμœΒΝ–¥πΑΗ «αΥ…ΩΈΧΟ±ξΉΦΝΖœΒΝ–¥πΑΗ
«αΥ…ΩΈΧΟ±ξΉΦΝΖœΒΝ–¥πΑΗ