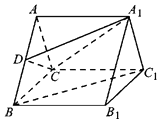
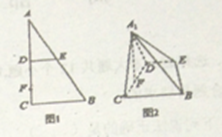
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΒγ…Χ÷–ΓΑΟ®ΙΖ¥σ’ΫΓ±‘ΎΫΎ»’ΤΎΦδΒΡΨΚ’υ“λ≥ΘΦΛΝ“Θ§‘ΎΗ’Ιΐ»ΞΒΡ618»ΪΟώΡξ÷–ΙΚΈοΫΎ÷–Θ§Ρ≥ΕΪΒ±»’ΫΜ“ΉΕν¥ο1195“Ύ‘ΣΘ§œ÷¥”ΗΟΒγ…ΧΓΑΕγ ÷Β≥Γ±÷–ΥφΜζ≥ι»Γ100ΟϊΙΥΩΆΫχ––ΜΊΖΟΘ§Α¥ΙΥΩΆΒΡΡξΝδΖ÷≥…ΝΥ6ΉιΘ§ΒΟΒΫ»γœ¬Υυ ΨΒΡΤΒ¬ ÷±ΖΫΆΦΘ° 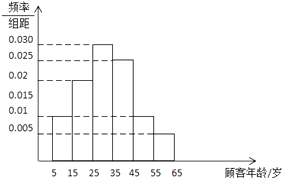
Θ®1Θ©«σΙΥΩΆΡξΝδΒΡ÷Ύ ΐΘ§÷–ΈΜ ΐΘ§ΤΫΨυ ΐΘ®ΟΩ“ΜΉι ΐΨί”Ο÷–ΒψΉω¥ζ±μΘ©ΘΜ
Θ®2Θ©”Ο―υ±Ψ ΐΨίΒΡΤΒ¬ ΙάΦΤΉήΧεΖ÷≤Φ÷–ΒΡΗ≈¬ Θ§‘ρ¥”»Ϊ≤ΩΙΥΩΆ÷–»Έ»Γ3»ΥΘ§Φ«ΥφΜζ±δΝΩXΈΣΙΥΩΆ÷–ΡξΝδ–Γ”Ύ25ΥξΒΡ»Υ ΐΘ§«σΥφΜζ±δΝΩXΒΡΖ÷≤ΦΝ–“‘ΦΑ ΐ―ßΤΎΆϊΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Θ§[25Θ§35Θ©Ε‘”ΠΒΡ–ΓΨΊ–ΈΉνΗΏΘ§
Γύ÷Ύ ΐΈΣm= ![]() =30Θ§
=30Θ§
”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΒΟΘΚ
0.01ΓΝ10+0.02ΓΝ10=0.3ΘΦ0.5Θ§
0.3+0.03ΓΝ10=0.6ΘΨ0.5Θ§
Γύ÷–ΈΜ ΐ‘Ύ«χΦδ[25Θ§35Θ©ΡΎΘ§…ηΈΣnΘ§
‘ρΘ®n©¹25Θ©ΓΝ0.03+0.3=0.5Θ§
ΫβΒΟnΓ÷31.7ΘΜ
ΤΫΨυ ΐΈΣ ![]() =0.01ΓΝ10ΓΝ10+0.02ΓΝ10ΓΝ20+0.03ΓΝ10ΓΝ30
=0.01ΓΝ10ΓΝ10+0.02ΓΝ10ΓΝ20+0.03ΓΝ10ΓΝ30
+0.025ΓΝ10ΓΝ40+0.01ΓΝ10ΓΝ50+0.005ΓΝ10ΓΝ60=32
Θ®2Θ©ΫβΘΚ”Ο―υ±ΨΤΒ¬ ΙάΦΤΉήΧεΤΒ¬ Θ§÷ΣΡξΝδ–Γ”Ύ25ΥξΒΡΗ≈¬ ΈΣ0.3Θ§«“XΓΪBΘ®3Θ§0.3Θ©Θ§
ΓύPΘ®X=0Θ©= ![]() Θ®1©¹0.3Θ©3=0.343Θ§
Θ®1©¹0.3Θ©3=0.343Θ§
PΘ®X=1Θ©= ![]() Θ®1©¹0.3Θ©20.3=0.441Θ§
Θ®1©¹0.3Θ©20.3=0.441Θ§
PΘ®X=2Θ©= ![]() Θ®1©¹0.3Θ©0.32=0.189Θ§
Θ®1©¹0.3Θ©0.32=0.189Θ§
PΘ®X=3Θ©= ![]() 0.33=0.027ΘΜ
0.33=0.027ΘΜ
ΓύXΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 0 | 1 | 2 | 3 |
P | 0.343 | 0.441 | 0.189 | 0.027 |
ΐ―ßΤΎΆϊΈΣEX=3ΓΝ0.3=0.9
ΓΨΫβΈωΓΩΘ®1Θ©ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Θ§ΗυΨί–ΓΨΊ–ΈΉνΗΏΒΡ“ΜΉιΒΉ±Ώ÷–ΒψΉχ±ξ«σ≥ω÷Ύ ΐΘ§ΗυΨί÷–ΈΜ ΐΝΫ±ΏΤΒ¬ œύΒ»«σ≥ω÷–ΈΜ ΐΒΡ÷ΒΘ§ΗυΨίΟΩ“ΜΉιΒΉ±Ώ÷–Βψ”κΕ‘”ΠΤΒ¬ ΒΡ≥ΥΜΐ«σΚΆ«σ≥ωΤΫΨυ ΐΘΜΘ®2Θ©”Ο―υ±ΨΤΒ¬ ΙάΦΤΉήΧεΤΒ¬ ΒΟΡξΝδ–Γ”Ύ25ΥξΒΡΗ≈¬ ÷ΒΘ§άϊ”ΟXΓΪBΘ®3Θ§0.3Θ©«σ≥ωXΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ÷ΒΘ°
ΓΨΩΦΒψΨΪΈωΓΩΙΊ”Ύ±ΨΧβΩΦ≤ιΒΡάκ…Δ–ΆΥφΜζ±δΝΩΦΑΤδΖ÷≤ΦΝ–Θ§–η“ΣΝΥΫβ‘Ύ…δΜςΓΔ≤ζΤΖΦλ―ιΒ»άΐΉ”÷–Θ§Ε‘”ΎΥφΜζ±δΝΩXΩ…Ρή»ΓΒΡ÷ΒΘ§Έ“Ο«Ω…“‘Α¥“ΜΕ®¥Έ–ρ“Μ“ΜΝ–≥ωΘ§’β―υΒΡΥφΜζ±δΝΩΫ–Ήωάκ…Δ–ΆΥφΜζ±δΝΩΘ°άκ…Δ–ΆΥφΜζ±δΝΩΒΡΖ÷≤ΦΝ–ΘΚ“ΜΑψΒΡ,…ηάκ…Δ–ΆΥφΜζ±δΝΩXΩ…Ρή»ΓΒΡ÷ΒΈΣx1,x2,.....,xi,......,xnΘ§X»ΓΟΩ“ΜΗω÷Β xi(i=1,2,......Θ©ΒΡΗ≈¬ P(ΠΈ=xiΘ©ΘΫPiΘ§‘ρ≥Τ±μΈΣάκ…Δ–ΆΥφΜζ±δΝΩX ΒΡΗ≈¬ Ζ÷≤ΦΘ§Φρ≥ΤΖ÷≤ΦΝ–≤≈ΡήΒΟ≥ω’ΐ»Ζ¥πΑΗΘ°

 ΚΘΒμΜΤΗ‘Οϊ ΠΒΦΚΫœΒΝ–¥πΑΗ
ΚΘΒμΜΤΗ‘Οϊ ΠΒΦΚΫœΒΝ–¥πΑΗ Τ’Ά®ΗΏ÷–Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗ
Τ’Ά®ΗΏ÷–Ά§≤ΫΝΖœΑ≤αœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥≥ß…ΧΈΣΝΥΫβ”ΟΜßΕ‘Τδ≤ζΤΖ «Ζώ¬ζ“βΘ§‘Ύ Ι”Ο≤ζΤΖΒΡ”ΟΜß÷–ΥφΜζΒς≤ιΝΥ80»ΥΘ§ΫαΙϊ»γœ¬±μΘΚ
Θ®1Θ©ΗυΨί…œ ωΘ§œ÷”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»ΓΕ‘≤ζΤΖ¬ζ“βΒΡ”ΟΜß5»ΥΘ§‘Ύ’β5»Υ÷–»Έ―Γ2»ΥΘ§«σ±Μ―Γ÷–ΒΡ«ΓΚΟ «Ρ–ΓΔ≈°”ΟΜßΗς1»ΥΒΡΗ≈¬ ΘΜ
Θ®2Θ©”–Εύ¥σΑ―Έ’»œΈΣ”ΟΜßΕ‘ΗΟ≤ζΤΖ «Ζώ¬ζ“β”κ”ΟΜß–‘±π”–ΙΊΘΩ«κΥΒΟςάμ”….
| 0.15 | 0Θ°10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ΉΔΘΚ ![]()