题目内容
【题目】已知函数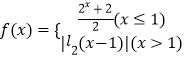 
，则函数 
的零点个数是（ ）
A.4
B.5
C.6
D.7
【答案】A
【解析】
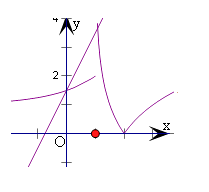
令t=f(x),F(x)=0，则f(t)2t 
=0，分别作出y=f(x)和直线y=2x+ ，由图象可得有两个交点,横坐标设为t1,t2，则t1=0,1<t2<2，
即有f(x)=0有一根；1<f(x)<2时,t2=f(x)有3个不等实根，综上可得F(x)=0的实根个数为4，即函数F(x)=f[f(x)]2f(x) 的零点个数是4.
所以答案是：A
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识，掌握二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点．
练习册系列答案
相关题目
【题目】某厂商为了解用户对其产品是否满意，在使用产品的用户中随机调查了80人，结果如下表：
（1）根据上述，现用分层抽样的方法抽取对产品满意的用户5人，在这5人中任选2人，求被选中的恰好是男、女用户各1人的概率；
（2）有多大把握认为用户对该产品是否满意与用户性别有关？请说明理由.
| 0.15 | 0．10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注： 
