题目内容
【题目】在直三棱柱ABC﹣A1B1C1中，∠ABC=90°，E、F分别为A1C1、B1C1的中点，D为棱CC1上任一点．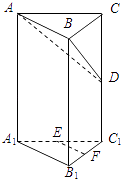 
（Ⅰ）求证：直线EF∥平面ABD；
（Ⅱ）求证：平面ABD⊥平面BCC1B1 ．
【答案】证明：（Ⅰ）因为E、F分别为A1C1，B1C1的中点，所以EF∥A1B1∥AB
而EF面ABD，AB面ABD，所以直线EF∥平面ABD
（Ⅱ）因为三棱柱ABC﹣A1B1C1为直三棱柱，所以AB⊥BB1，又AB⊥BC，
而BB1面BCC1B1，BC面BCC1B1，且BB1∩BC=B，所以AB⊥面BCC1B1
又AB面ABD，所以平面ABD⊥平面BCC1B1
【解析】（I）因为E、F分别为A1C1，B1C1的中点，由三角形中位线定理，我们易证明EF∥AB，根据线面平行的判定定理，我们易得直线EF∥平面ABD；（Ⅱ）由已知中直三棱柱ABC﹣A1B1C1中，∠ABC=90°，结合线面垂直判定定理，我们易得AB⊥面BCC1B1，再由面面垂直判定定理，即可得到平面ABD⊥平面BCC1B1．
练习册系列答案
相关题目
