题目内容
3.已知函数f(x)=x4-4x3+tx2+6(t∈R).①若t=4,求f(x)的单调区间;②若f(x)在x=-1处取得极值,求f(x)在区间[-2,1]上的最大值与最小值.分析 ①当t=4时,f′(x)=4x3-12x2+8x=4x(x-1)(x-2),分别解出:f′(x)>0,f′(x)<0,解出即可.
②f′(x)=4x3-12x2+2tx=4x(x2-3x+$\frac{t}{2}$),由已知f(-1)=0,t=-8,此时f′(x)=4x(x+1)(x-4),分别解出:f′(x)<0,f′(x)>0.可得单调性,进而得出极值与最值.
解答 解:①当t=4时,f′(x)=4x3-12x2+8x=4x(x-1)(x-2),
由f′(x)>0解得x∈(0,1)∪(2,+∞),
∴f(x)的增区间是(0,1)和(2,+∞);
由f′(x)<0,解得x∈(-∞,0)∪(1,2),
∴f(x)的减区间是(-∞,0)和(1,2).
②f′(x)=4x3-12x2+2tx=4x(x2-3x+$\frac{t}{2}$),由已知f(-1)=0,t=-8,
此时f′(x)=4x(x+1)(x-4),
则当x∈(-2,-1)时,f′(x)<0;x∈(-1,0)时,f′(x)>0;x∈(0,1)时,f′(x)<0.
∴f(x)在x=-1处取得极小值3,在x=0处取得极大值6,
而f(-2)=22,f(1)=-5,
则f(x)在[-2,1]上的最大值是22,最小值时-5.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.执行如图所示的程序框图,输出的S的值是( )
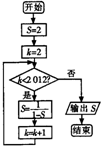

| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |