题目内容
13.在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,AB=BC=2,AA1=1,E为BB1的中点,求证:平面AEC1⊥平面AA1C1C.分析 取AC1的中点F,连接EF,A1F,A1E,运用直角三角形的性质和勾股定理,由线面垂直的判定,可得EF⊥平面AA1C1C,再由面面垂直的判定定理,即可得证.
解答 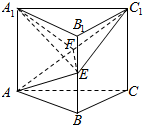 证明:取AC1的中点F,连接EF,A1F,A1E,
证明:取AC1的中点F,连接EF,A1F,A1E,
在直角三角形ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{4+\frac{1}{4}}$=$\frac{\sqrt{17}}{2}$,
在直角三角形B1C1E中,C1E=$\sqrt{{B}_{1}{E}^{2}+{B}_{1}{{C}_{1}}^{2}}$
=$\sqrt{4+\frac{1}{4}}$=$\frac{\sqrt{17}}{2}$,
即有△ACE1为等腰三角形,且FE⊥AC1,
FE=$\sqrt{A{E}^{2}-\frac{1}{4}A{{C}_{1}}^{2}}$=$\sqrt{4+\frac{1}{4}-\frac{1}{4}(4+4+1)}$=$\sqrt{2}$,
在直角三角形AA1C1中,A1F=$\frac{1}{2}$AC1=$\frac{3}{2}$,
又A1E=$\sqrt{4+\frac{1}{4}}$=$\frac{\sqrt{17}}{2}$,
由A1E2=FE2+A1F2,可得EF⊥A1F,
又FE⊥AC1,即有EF⊥平面AA1C1C.
由于EF?平面AEC1,
则平面AEC1⊥平面AA1C1C.
点评 本题考查面面垂直的判定定理的运用,考查空间直线和平面的位置关系,考查运算和推理能力,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在平面,AB=2,AF=1,
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在平面,AB=2,AF=1,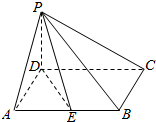 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.