题目内容
12.已知等边△ABC的边长为2,M为AC中点,N为BC中点,$\overrightarrow{AN}$$•\overrightarrow{BM}$=-$\frac{3}{2}$.分析 由条件利用两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义求得$\overrightarrow{AN}$=$\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$•($\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$) 的值.
解答 解:由题意可得$\overrightarrow{AN}$=$\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$•($\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{{\overrightarrow{AC}}^{2}-\overrightarrow{AB}•\overrightarrow{AC}-{2\overrightarrow{AB}}^{2}}{4}$
=$\frac{\frac{4}{2}-\frac{1}{2}×2×2×cos60°-4}{4}$=-$\frac{3}{2}$,
故答案为:-$\frac{3}{2}$.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在平面,AB=2,AF=1,
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在平面,AB=2,AF=1,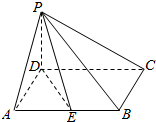 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,点E为AB中点.