题目内容
14.设△ABC的内角A,B,C所对应的边长分别是a,b,c且cosB=$\frac{3}{5}$,b=2(Ⅰ)当A=30°时,求a的值;
(Ⅱ)当△ABC的面积为3时,求a+c的值.
分析 (Ⅰ)由cosB=$\frac{3}{5}$,B∈(0,π),可得sinB=$\sqrt{1-co{s}^{2}B}$,再利用正弦定理即可得出.
(Ⅱ)由S△ABC=$\frac{1}{2}acsinB$=3,可得ac=$\frac{15}{2}$.再利用余弦定理即可得出.
解答 解:(Ⅰ)∵cosB=$\frac{3}{5}$,B∈(0,π),
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4}{5}$,
由正弦定理可知:$\frac{a}{sin3{0}^{°}}=\frac{2}{\frac{4}{5}}$,
∴a=$\frac{5}{4}$.
(Ⅱ)∵S△ABC=$\frac{1}{2}acsinB$=$\frac{1}{2}ac×\frac{4}{5}$=3,
∴ac=$\frac{15}{2}$.
由余弦定理得:b2=a2+c2-2accosB=(a+c)2-2ac-2ac×$\frac{3}{5}$=4,
∴(a+c)2=$\frac{16}{5}×\frac{15}{2}$+4=28,
故:a+c=2$\sqrt{7}$.
点评 本题考查了正弦定理与余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
4.函数f(x)=$\sqrt{2x}$从x=$\frac{1}{2}$到x=2的平均变化率为( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\sqrt{2}$ |
6.若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[-1,0]时,f(x)=-x,则f(2011)=( )
| A. | 1 | B. | 0 | C. | 2010 | D. | 2011 |
3.在△ABC中,∠A=120°,AC=$\sqrt{3}$,AB=2$\sqrt{3}$,O为BC的中点,则AO=( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{9}{4}$ | D. | 9 |
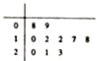 现从某1000件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,
现从某1000件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,