题目内容
5. 现从某1000件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,
现从某1000件中药材中随机抽取10件,以这10件中药材的重量(单位:克)作为样本,样本数据的茎叶图如图,(1)求样本数据的中位数、平均数,并估计这1000件中药材的总重量;
(2)记重量在15克以上的中药材为优等品,在该样本的优等品中,随机抽取2件,求这2件中药材的重量之差不超过2克的概率.
分析 (1)根据茎叶图数据直接求样本数据的中位数、平均数即可;
(2)列举从10件中药材的优等品中随机抽取2件的所有基本事件,找出2件优等品的重量之差不超过2克所包含的事件,利用古典概型概率公式计算即可
解答 解:(1)样本数据的中位数是$\frac{12+17}{2}$=14.5,
样本数据的平均数是$\frac{1}{10}$(8+9+10+12+12+17+18+20+21+23)=15;
根据样本数据估计总体的思想可得,这1000件中药材重量的平均数是15克,
因此,估计这1000件中药材的总重量约为1000×15=15000克.
(2)这10件中药材的优等品的重量有17克、18克、20克、21克、23克.
从10件中药材的优等品中随机抽取2件,所有基本事件有:
(17,18),(17,20),(17,21),(17,23),(18,20),(18,21),
(18,23),(20,21),(20,23),(21,23)共10个.
记“2件优等品的重量之差不超过2克”为事件A,
则事件A的基本事件有:(17,18),(18,20),),(20,21),(21,23)共4个.
∴P(A)=$\frac{4}{10}$=$\frac{2}{5}$.
∴这2件中药材的重量之差不超过2克的概率$\frac{2}{5}$.
点评 本题考查茎叶图、平均数、中位数、古典概型等知识,以及数据处理能力,样本估计总体的数学思想.属于中档题

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
20. 已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
 已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )
已知函数f(x)=$\sqrt{3}$sin(ωx+φ)(ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=$\sqrt{3}$cos(ωx+$\frac{φ}{2}$)的图象,只需将f(x)的图象( )| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向左平移$\frac{5π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{5π}{12}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |
17.已知函数f(x)=ln(x+1)+2x-m(m∈R)的一个零点附近的函数值的参考数据如表:
由二分法,方程ln(x+1)+2x-m=0的近似解(精确度0.05)可能是( )
| x | 0 | 0.5 | 0.53125 | 0.5625 | 0.625 | 0.75 | 1 |
| f(x) | -1.307 | -0.084 | -0.009 | 0.066 | 0.215 | 0.512 | 1.099 |
| A. | 0.625 | B. | -0.009 | C. | 0.5625 | D. | 0.066 |
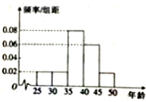 2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )
2015年某企业员工有500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.现在要从年龄较小的第1,3,4组中用分层抽样的方法抽取16人,则在第4组抽取的人数为( )