题目内容
在极坐标系中，已知曲线C1：ρ＝12sinθ，曲线C2：ρ＝12cos
.
(1)求曲线C1和C2的直角坐标方程；
(2)若P、Q分别是曲线C1和C2上的动点，求PQ的最大值．
.(1)求曲线C1和C2的直角坐标方程；
(2)若P、Q分别是曲线C1和C2上的动点，求PQ的最大值．
（1）曲线C1的直角坐标方程为x2＋(y－6)2＝36.C2的直角坐标方程为(x－3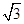
)2＋(y－3)2＝36（2）18
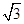)2＋(y－3)2＝36（2）18(1)因为ρ＝12sinθ，所以ρ2＝12ρsinθ，所以x2＋y2－12y＝0，即曲线C1的直角坐标方程为x2＋(y－6)2＝36.又ρ＝12cos，所以ρ2＝12ρ
，所以x2＋y2－6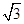x－6y＝0，即曲线C2的直角坐标方程为(x－3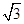)2＋(y－3)2＝36.
(2)PQmax＝6＋6＋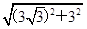
＝18
，所以ρ2＝12ρ，所以x2＋y2－6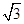x－6y＝0，即曲线C2的直角坐标方程为(x－3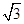)2＋(y－3)2＝36.(2)PQmax＝6＋6＋
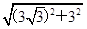＝18
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
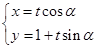（t为参数，0≤α<π）。以原点为极点，x轴的正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
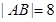，求α的值。
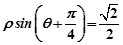，则点A(2，
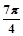)到这条直线的距离为 .
（
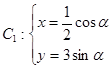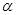为参数），曲线
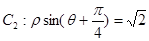，将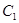
的横坐标伸长为原来的2倍，纵坐标缩短为原来的
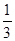得到曲线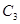
.
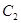的直角坐标方程；
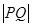的最小值，并求此时的P的坐标．
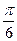)到直线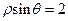
的距离等于 .
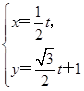(t为参数)，求直线l被曲线C截得的线段的长度．
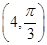，求|CP|.
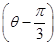＝a，a∈R，圆C的参数方程是
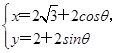(θ为参数)．若圆C关于直线l对称，则a＝________.