题目内容
16.若集合{x,y,x}={1,2,3},且下列三个关系:①x=1;②y≠1③z=2有且只有一个是正确的,求符合条件的有序数组(x,y,z)分析 根据条件,在三个关系中只有一个正确,不妨设①正确,②③错误,判断这种情况是否存在,并确定x,y,z的值.同样的方法,另外的情况便是:假设②正确,①③错误,和③正确,①②错误,这样求出每种情况的x,y,z,从而得出有序数组(x,y,z).
解答 解:(1)若x=1正确,则y≠1正确,不符合只有一个正确;
(2)若y≠1正确,则x≠1,z≠2;
∴z=1,x=2,y=3,或z=1,x=3,y=2;
(3)若z=2正确,则x≠1,y=1;
∴x=3,y=1,z=2;
∴符合条件的有序数组(x,y,z)为:(2,3,1),(3,2,1),(3,1,2).
点评 考查集合,元素的概念,以及元素与集合的关系,并理解有序实数组的概念.

练习册系列答案
相关题目
7.如图,阴影部分可表示为( )
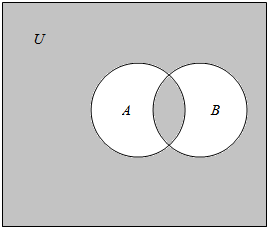

| A. | (A∪B)∩(∁U(A∩B)) | B. | ∁U(A∪B) | C. | ∁U(A∩∁UB) | D. | [∁U(A∪B)]∪(A∩B) |