题目内容
15.已知函数f(x)=-2x2+22x,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N+)均在函数y=f(x)的图象上.(1)求数列{an}的通项公式an及前n项和Sn;
(2)存在k∈N+,使得$\frac{S_1}{1}+\frac{S_2}{2}+…+\frac{S_n}{n}<k$对任意n∈N*恒成立,求出k的最小值.
分析 (1)通过将点Pn(n,Sn)(n∈N+)代入f(x)=-2x2+22x可知数列{an}的前n项和Sn=-2n2+22n,利用an+1=Sn+1-Sn可知an+1=-4(n+1)+24,进而可知数列{an}的通项公式an=-4n+24;
(2)通过Sn=-2n2+22n可知$\frac{{S}_{n}}{n}$=-2n+22,进而可知$\frac{{S}_{1}}{1}$+$\frac{{S}_{2}}{2}$+…+$\frac{{S}_{11}}{11}$<k,进而计算可得结论.
解答 解:(1)∵点Pn(n,Sn)(n∈N+)均在函数y=f(x)=-2x2+22x的图象上,
∴数列{an}的前n项和Sn=-2n2+22n,
∴an+1=Sn+1-Sn
=-2(n+1)2+22(n+1)+2n2-22n
=-4n+20
=-4(n+1)+24,
又∵a1=-2+22=20满足上式,
∴数列{an}的通项公式an=-4n+24;
(2)∵Sn=-2n2+22n,
∴$\frac{{S}_{n}}{n}$=-2n+22,
∴当n=11时$\frac{{S}_{n}}{n}$=0,当n>11时$\frac{{S}_{n}}{n}$<0,当n<11时$\frac{{S}_{n}}{n}$>0,
又∵$\frac{{S}_{1}}{1}$+$\frac{{S}_{2}}{2}$+…+$\frac{{S}_{11}}{11}$=-2(1+2+…+11)+22×11
=-2×$\frac{11×12}{2}$+22×11
=110,
∴k的最小值为111.
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
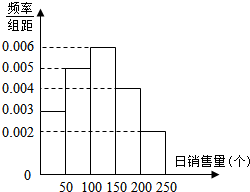 某校小卖部根据以往某种商品的销售记录,绘制了如下的日销售量频率分布直方图.若以日销售量的频率为概率,假设每天的销售量是相互独立的.结合直方图相关数据,以此来估计未来连续3天日销售量.
某校小卖部根据以往某种商品的销售记录,绘制了如下的日销售量频率分布直方图.若以日销售量的频率为概率,假设每天的销售量是相互独立的.结合直方图相关数据,以此来估计未来连续3天日销售量.