Question

4．若f（x）=$\left\{\begin{array}{l}{（x-1）^{2}\\;x≥0}\\{x+1\\;x＜0}\end{array}\right.$，则f（x）的单调增区间是（-∞，0），[1，+∞），单调减区间是[0，1]．

Answer 1

分析 作出函数f（x）的图象，结合图象进行判断即可．

解答 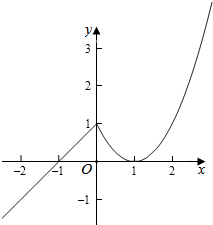解：函数的图象为：
则当x＜0时，函数为增函数，
当x≥0时，f（x）=（x-1）²，对称轴为x=1，
则当0≤x≤1时，函数单调递减，
当x≥1时，函数单调递增，
故函数的单调递增区间为（-∞，0），[1，+∞），
单调递减区间为[0，1]，
故答案为：（-∞，0），[1，+∞）；[0，1]

点评 本题主要考查函数单调区间的求解，利用函数图象结合一元二次函数的单调性的性质是解决本题的关键．