题目内容
函数f(x)=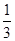 x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是________.
x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是________.
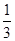 x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是________.
x3-x2+ax-5在区间[-1,2]上不单调,则实数a的取值范围是________.(-3,1)
∵f(x)=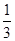 x3-x2+ax-5,∴f′(x)=x2-2x+a=(x-1)2+a-1,如果函数f(x)=
x3-x2+ax-5,∴f′(x)=x2-2x+a=(x-1)2+a-1,如果函数f(x)=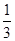 x3-x2+ax-5在区间[-1,2]上单调,那么a-1≥0或f′(-1)=3+a≤0且f′(2)=a≤0,∴a≥1或a≤-3.于是满足条件的a∈(-3,1).
x3-x2+ax-5在区间[-1,2]上单调,那么a-1≥0或f′(-1)=3+a≤0且f′(2)=a≤0,∴a≥1或a≤-3.于是满足条件的a∈(-3,1).
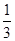 x3-x2+ax-5,∴f′(x)=x2-2x+a=(x-1)2+a-1,如果函数f(x)=
x3-x2+ax-5,∴f′(x)=x2-2x+a=(x-1)2+a-1,如果函数f(x)=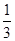 x3-x2+ax-5在区间[-1,2]上单调,那么a-1≥0或f′(-1)=3+a≤0且f′(2)=a≤0,∴a≥1或a≤-3.于是满足条件的a∈(-3,1).
x3-x2+ax-5在区间[-1,2]上单调,那么a-1≥0或f′(-1)=3+a≤0且f′(2)=a≤0,∴a≥1或a≤-3.于是满足条件的a∈(-3,1).
练习册系列答案
相关题目
 在( )
在( )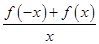 <0的解集为________.
<0的解集为________.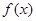 是定义在
是定义在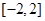 上的函数,且对任意实数
上的函数,且对任意实数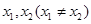 ,恒有
,恒有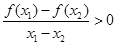 ,且
,且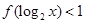 的解为
的解为 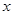 ,有
,有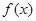 为奇函数,
为奇函数,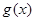 为偶函数,且
为偶函数,且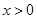 时,
时,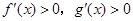 ,则
,则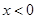 时( )
时( )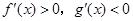
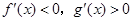
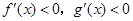 导数
导数 ﹣1的图象大致是( )
﹣1的图象大致是( )
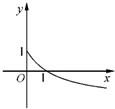
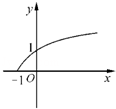
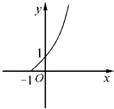
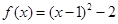 的递增区间是___________________ .
的递增区间是___________________ .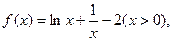 则函数
则函数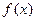 的零点个数是( )
的零点个数是( )