题目内容
设数列{an}是以2为首项，1为公差的等差数，{bn}是以1为首项，2为公比的等比数列，则ba1+ba2+ba3+…+ba6等于（ ）
| A．78 | B．84 | C．124 | D．126 |
∵数列{an}是以2为首项，1为公差的等差数列，∴an=2+（n-1）×1=n+1．
则a1=2，a2=3，a3=4，a4=5，a5=6，a6=7，
{bn}是以1为首项，2为公比的等比数列，则bn=1×2n-1=2n-1，
∴ba1+ba2+…+ba6=b2+b3+b4+b5+b6+b7
=2+4+8+16+32+64=126．
故选：D．
则a1=2，a2=3，a3=4，a4=5，a5=6，a6=7，
{bn}是以1为首项，2为公比的等比数列，则bn=1×2n-1=2n-1，
∴ba1+ba2+…+ba6=b2+b3+b4+b5+b6+b7
=2+4+8+16+32+64=126．
故选：D．
练习册系列答案
相关题目
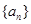的首项
.
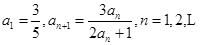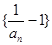是等比数列，并求出
；
.
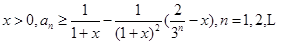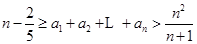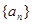的前n项和为
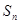，且
（
）.
，
，
，
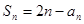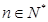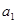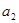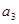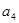的值；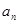
的表达式，并加以证明。