题目内容
已知数列{an }的前n项和为Sn,满足an ¹ 0, ,
, .
.
(1)求证: ;
;
(2)设 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
 ,
, .
.(1)求证:
 ;
;(2)设
 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.(1)见解析(2)Tn=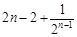
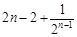
试题分析:(1)由
 ,变形为
,变形为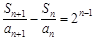 ,然后利用累加法可证得结果.
,然后利用累加法可证得结果.(2)由
 ,
,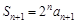 .两式相减得
.两式相减得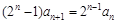 ,即
,即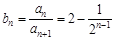 ,然后利用等差等比数列的前n项和公式即可求得结果.
,然后利用等差等比数列的前n项和公式即可求得结果.试题解析:(1)证明:∵
 ,an ¹ 0,
,an ¹ 0,∴
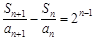 .
. 则
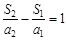 ,
,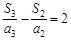 ,…,
,…,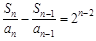 (n≥2,
(n≥2, ).
).以上各式相加,得
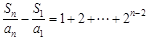 .
. ∵
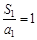 ,∴
,∴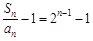 .
. ∴
 (n≥2,
(n≥2, ).
). ∵n = 1时上式也成立,∴
 (
( ).
). (2)∵
 ,
,∴
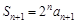 .
.两式相减,得
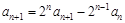 .
. 即
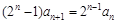 .
. 则
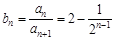 .
. 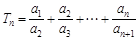 =
=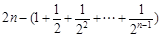 =
=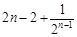 .
. 
练习册系列答案
相关题目
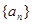 的前n项和为
的前n项和为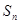 ,且
,且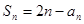 (
(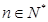 ).
).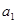 ,
,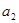 ,
,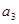 ,
,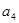 的值;
的值;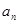 的表达式,并加以证明。
的表达式,并加以证明。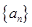 满足
满足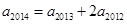 ,且
,且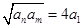 ,则
,则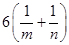 的最小值( )
的最小值( )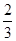
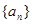 中,
中,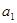 =2,
=2,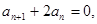 则
则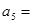 ________.
________.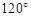 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来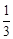 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为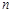 级分形图.
级分形图.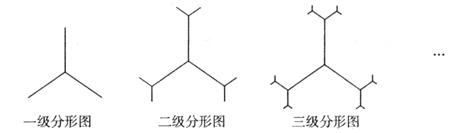
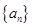 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且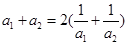 ,
,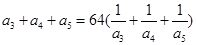
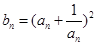 求数列
求数列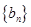 的前
的前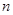 项和
项和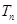 .
. 中,若
中,若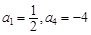 ,则
,则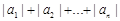 =____________.
=____________.