题目内容
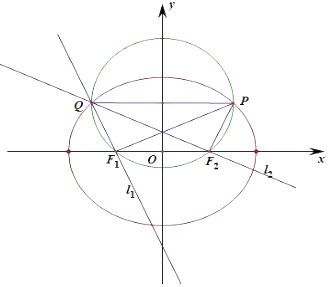
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为 ![]() ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1 , 过点F2作直线PF2的垂线l2 .
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1 , 过点F2作直线PF2的垂线l2 .
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线l1 , l2的交点Q在椭圆E上,求点P的坐标.
【答案】解:(Ⅰ)由题意可知:椭圆的离心率e= ![]() =
= ![]() ,则a=2c,①
,则a=2c,①
椭圆的准线方程x=± ![]() ,由2×
,由2× ![]() =8,②
=8,②
由①②解得:a=2,c=1,
则b2=a2﹣c2=3,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)设P(x0 , y0),则直线PF2的斜率 ![]() =
= ![]() ,
,
则直线l2的斜率k2=﹣ ![]() ,直线l2的方程y=﹣
,直线l2的方程y=﹣ ![]() (x﹣1),
(x﹣1),
直线PF1的斜率 ![]() =
= ![]() ,
,
则直线l2的斜率k2=﹣ ![]() ,直线l2的方程y=﹣
,直线l2的方程y=﹣ ![]() (x+1),
(x+1),
联立 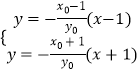 ,解得:
,解得: 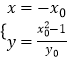 ,则Q(﹣x0 ,
,则Q(﹣x0 , ![]() ),
),
由Q在椭圆上,则y0= ![]() ,则y02=x02﹣1,
,则y02=x02﹣1,
则 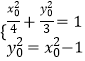 ,解得:
,解得: 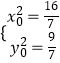 ,则
,则 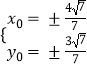 ,
,
∴P( ![]() ,
, ![]() )或P(﹣
)或P(﹣ ![]() ,
, ![]() )或P(
)或P( ![]() ,﹣
,﹣ ![]() )或P(﹣
)或P(﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(Ⅰ)由椭圆的离心率公式求得a=2c,由椭圆的准线方程x=± ![]() ,则2×
,则2× ![]() =8,即可求得a和c的值,则b2=a2﹣c2=3,即可求得椭圆方程;
=8,即可求得a和c的值,则b2=a2﹣c2=3,即可求得椭圆方程;
(Ⅱ)设P点坐标,分别求得直线PF2的斜率及直线PF1的斜率,则即可求得l2及l1的斜率及方程,联立求得Q点坐标,由Q在椭圆方程,求得y02=x02﹣1,联立即可求得P点坐标;
【考点精析】根据题目的已知条件,利用点斜式方程的相关知识可以得到问题的答案,需要掌握直线的点斜式方程:直线![]() 经过点
经过点![]() ,且斜率为
,且斜率为![]() 则:
则:![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】已知一个口袋有m个白球,n个黑球(m,n∈N* , n≥2),这些球除颜色外全部相同.现将口袋中的球随机的逐个取出,并放入如图所示的编号为1,2,3,…,m+n的抽屉内,其中第k次取出的球放入编号为k的抽屉(k=1,2,3,…,m+n).
1 | 2 | 3 | … | m+n |
(Ⅰ)试求编号为2的抽屉内放的是黑球的概率p;
(Ⅱ)随机变量x表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是X的数学期望,证明E(X)< ![]() .
.