题目内容
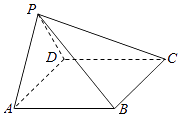
【题目】如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD. 求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.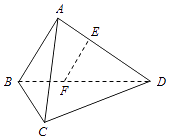
【答案】证明:(Ⅰ)因为AB⊥AD,EF⊥AD,且A、B、E、F四点共面, 所以AB∥EF,
又因为EF平面ABC,AB平面ABC,
所以由线面平行判定定理可知:EF∥平面ABC;
(Ⅱ)在线段CD上取点G,连结FG、EG使得FG∥BC,则EG∥AC,
因为BC⊥BD,所以FG⊥BC,
又因为平面ABD⊥平面BCD,
所以FG⊥平面ABD,所以FG⊥AD,
又因为AD⊥EF,且EF∩FG=F,
所以AD⊥平面EFG,所以AD⊥EG,
故AD⊥AC.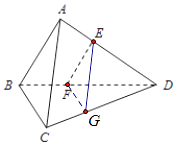
【解析】(Ⅰ)利用AB∥EF及线面平行判定定理可得结论; (Ⅱ)通过取线段CD上点G,连结FG、EG使得FG∥BC,则EG∥AC,利用线面垂直的性质定理可知FG⊥AD,结合线面垂直的判定定理可知AD⊥平面EFG,从而可得结论.
【考点精析】利用空间中直线与直线之间的位置关系和直线与平面平行的判定对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
相关题目