题目内容
【题目】已知某几何体的三视图和直观图如图所示,其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
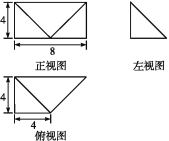
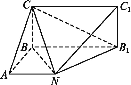
(1)证明:平面BCN⊥平面C1NB1;
(2)求二面角C-NB1-C1的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)建立空间直角坐标系,根据坐标运算,求得直线与平面的垂直,进而判断平面与平面的垂直。
(2)根据空间直角坐标系,求出两个平面的法向量,进而利用两个平面的法向量求出两个平面的二面角大小。
(1)证明∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两垂直.

以![]() 分别作为x,y,z轴的正方向,建立如图所示的空间直角坐标系,
分别作为x,y,z轴的正方向,建立如图所示的空间直角坐标系,
则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4),![]() =-16+16+0=0,
=-16+16+0=0,![]() =0,
=0,
∴NB⊥NB1,NB⊥B1C1.
又NB1与B1C1相交于B1,∴NB⊥平面C1NB1.
又NB平面BCN.
∴平面BCN⊥平面C1NB1.
(2)解设n=(x,y,z)是平面NCB1的一个法向量,![]() =(4,4,-4),
=(4,4,-4),![]() =(4,-4,0),
=(4,-4,0),
则
取x=1,得n=(1,1,2).
由(1)知![]() =(4,4,0)是平面C1B1N的一个法向量,
=(4,4,0)是平面C1B1N的一个法向量,
cos<n,![]() >=
>=![]() .
.
故二面角C-NB1-C1的余弦值为![]() .
.

练习册系列答案
相关题目


