题目内容
5.求下列函数的定义域:(1)y=$\frac{1}{lo{g}_{3}(3x-2)}$;
(2)y=log(2x-1)(-4x+8).
分析 通过对数的真数与底数的范围.列出不等式求解函数的值域、
解答 解:(1)y=$\frac{1}{lo{g}_{3}(3x-2)}$;函数有意义可得$\left\{\begin{array}{l}3x-2>0\\ 3x-2≠1\end{array}\right.$,解得:x$>\frac{2}{3}$且x≠1,
函数的定义域为:{x|x$>\frac{2}{3}$且x≠1}.
(2)函数y=log(2x-1)(-4x+8)有意义,可得:$\left\{\begin{array}{l}8-4x>0\\ 2x-1≠1\\ 2x-1>0\end{array}\right.$.解得:$\frac{1}{2}<x<1$或1<x<2.
函数的定义域为:{x|$\frac{1}{2}<x<1$或1<x<2}.
点评 本题考查函数的定义域的求法,对数函数的定义域,考查计算能力.

练习册系列答案
相关题目
15.已知奇函数f(x)在(0,+∞)上是增函数,且f(2)=0,则不等式x[f(x)-f(-x)]<0的解集为( )
| A. | {x|-2<x<0或x>2} | B. | {x|x<-2或0<x<2} | C. | {x|x<-2或x>2} | D. | {x|-2<x<0或0<x<2} |
10.(1+x)+(1+x)2+…+(1+x)n的所有二项式的各项系数和是( )
| A. | 2n+1 | B. | 2n+1+1 | C. | 2n+1-1 | D. | 2n+1-2 |
7.曲线C以双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}$=1的右焦点F为焦点,曲线C上的点到焦点F的距离与到直线x=-2的距离相等,则曲线C上的任意一点P到y轴的距离与到直线x-y+4=0的距离和的最小值为( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{2}$-1 | C. | 3$\sqrt{2}$+2 | D. | 3$\sqrt{2}$-2 |
4.已知函数y=-x2+3x,直线l1:x=t和l2:x=t+1(其中0≤t≤2,t为常数),若直线l1,l2,x轴与函数y=f(x)的图象所围成的封闭图形的面积为S,则S的最大值为( )
| A. | 2 | B. | $\frac{11}{6}$ | C. | $\frac{13}{6}$ | D. | 3 |
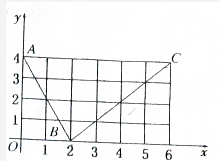 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).