题目内容
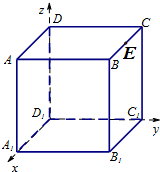
5.已知某几何体由正方体和直三棱柱组成,其三视图和直观图如图所示.记直观图中从点B出发沿棱柱的侧面到达PD1的中点R的最短距离为d,则d2=$\frac{25}{2}+6\sqrt{2}$.
分析 沿BB1剪开,画出侧面展开图,然后求出最小值即可.
解答 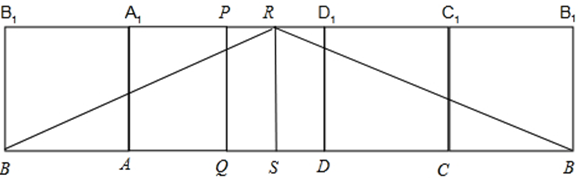 解:由三视图可知几何体是由一个正方体与一个直三棱柱组成的组合体,
解:由三视图可知几何体是由一个正方体与一个直三棱柱组成的组合体,
正方体的棱长为2,直三棱柱的底面边长为:$\sqrt{2},\sqrt{2},2$,高为2.
沿BB1剪开,画出侧面展开图,如图:
左侧BR最小,d=$\sqrt{{2}^{2}+({2+\frac{3\sqrt{2}}{2})}^{2}}$,
d2=${2}^{2}+({2+\frac{3\sqrt{2}}{2})}^{2}$=$\frac{25}{2}+6\sqrt{2}$.
故答案为:$\frac{25}{2}+6\sqrt{2}$.
点评 本题考查几何体的侧面展开图的应用,距离的最小值的求法,考查空间想象能力以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.有4块大小不同的试验田,要种不同的3种蔬菜,若每块最多种一种蔬菜,同一种蔬菜都得种入同一块田里.则不同的种植方式的种数是( )
| A. | ${C}_{4}^{3}$ | B. | A43 | C. | 43 | D. | 34 |
15.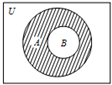 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )| A. | {x|1<x<3} | B. | {x|1<x≤3} | C. | {x|1≤x<3} | D. | {x|1≤x≤3} |