题目内容
10.椭圆 $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1内一点P(4,2),过点P的弦AB恰好被点P平分,则直线AB的方程为x+2y-8=0.分析 设A(x1,y1),B(x2,y2).可得由中点坐标公式可得4=$\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$=2,又kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$.将A,B坐标代入椭圆方程,相减即可得到直线AB的斜率,再由点斜式方程,即可得到所求直线方程.
解答 解:设A(x1,y1),B(x2,y2).
由中点坐标公式可得,4=$\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$=2,
又kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$.
∵$\frac{{{x}_{1}}^{2}}{36}$+$\frac{{{y}_{1}}^{2}}{9}$=1,$\frac{{{x}_{2}}^{2}}{36}$+$\frac{{{y}_{2}}^{2}}{9}$=1.
∴两式相减可得,$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{36}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$=0.
∴$\frac{{x}_{1}-{x}_{2}}{9}$+$\frac{2({y}_{1}-{y}_{2})}{9}$=0,
解得kAB=-$\frac{1}{2}$.
∴直线AB的方程为y-2=-$\frac{1}{2}$(x-4),化为x+2y-8=0.
故答案为:x+2y-4=0.
点评 本题考查了“点差法”、中点坐标公式、斜率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知F1、F2是椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的两个焦点,A为椭圆上一点,则△AF1F2的周长为( )
| A. | 4$\sqrt{6}$ | B. | 12 | C. | 14 | D. | 24 |
19.设$a={(\frac{2}{3})^x}$,$b={(\frac{3}{2})^{x-1}}$,$c={log_{\frac{2}{3}}}x$,若x>1,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
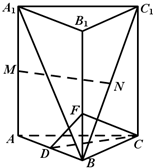 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.