题目内容
19.设$a={(\frac{2}{3})^x}$,$b={(\frac{3}{2})^{x-1}}$,$c={log_{\frac{2}{3}}}x$,若x>1,则a,b,c的大小关系是( )| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵$a={(\frac{2}{3})^x}$,$b={(\frac{3}{2})^{x-1}}$,$c={log_{\frac{2}{3}}}x$,x>1,
∴$0<a<\frac{2}{3}$,b>1,c<0,
∴b>a>c.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若不等式x2-ax+a≤1有解,则a的取值范围为( )
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a∈R |
4.芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如下表:
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a•bt,Q=alogbt,并说明理由;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
| t | 50 | 110 | 250 |
| Q | 150 | 108 | 150 |
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
11.河南省2013级高中学业水平考试在2015年1月16日至18日共考试三天,需考语文、数学、英语、物理、化学、生物、政治、历史、地理九门学科,若语文、数学、英语必须安排在下午,每天上午安排其余的六门学科,且每天上午考两门,下午考一门,问有多少种安排考试顺序的方法( )
| A. | 540 | B. | 720 | C. | 3240 | D. | 4320 |
8.已知tanα,tanβ是关于x的方程x2+(logaM+logbM)x-logaM•logbM=0两个根,其中a,b,M均不为1的正数,若sinαcosβ+cosαsinβ=2sinαsinβ,则a,b,M满足的关系是( )
| A. | $\frac{a+b}{2}$=M | B. | $\sqrt{ab}$=M | C. | a+b=M | D. | ab=M |
9.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则点C到平面BC1D的距离等于( )


| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{9}$ |
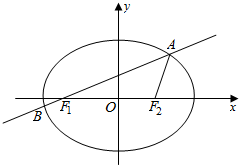 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.