题目内容
15.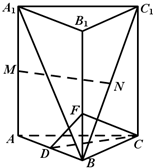 如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,D、M、N分别是AB、AA1、BC1的中点.(Ⅰ)求证:MN∥平面ABC;
(Ⅱ)再若AC=BC,BB1=$\sqrt{2}$AB,试在BB1上找一点F,使A1B⊥平面CDF,并证明你的结论.
分析 (Ⅰ)连接A1H(H为B1C1的中点),由M、N分别为AA1、BC1的中点可得,MN∥A1H,又A1H?平面A1B1C1,MN?平面A1B1C1,即可证明MN∥平面ABC.
(Ⅱ)作DE⊥A1B交A1B于E,延长DE交BB1于F,连接CF,则A1B⊥平面CDF,点F即为所求,根据CD⊥平面AA1BB,A1B?平面AA1B1B,则CD⊥A1B,A1B⊥DF,DF∩CD=D,满足线面垂直的判定定理,则A1B⊥平面CDF.
解答 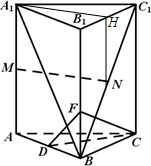 解:(Ⅰ)证明:连接A1H(H为B1C1的中点),由M、N分别为AA1、BC1的中点可得,
解:(Ⅰ)证明:连接A1H(H为B1C1的中点),由M、N分别为AA1、BC1的中点可得,
MN∥A1H,又∵A1H?平面A1B1C1,MN?平面A1B1C1,
∴MN∥平面A1B1C1.
∴由ABC-A1B1C1是直三棱柱,从而有MN∥平面ABC;
(Ⅱ)解:作DE⊥A1B交A1B于E,延长DE交BB1于F,连接CF,则A1B⊥平面CDF,点F即为所求.
∵CD⊥平面AA1B1B,A1B?平面AA1B1B,
∴CD⊥A1B.又A1B⊥DF,DF∩CD=D,
∴A1B⊥平面CDF.
∴此时点F为靠近B的四等分点.
点评 本题主要考查了直线与平面垂直的判定,考查了空间想象能力和推理论证能力,应熟练记忆直线与平面垂直的判定定理,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
5.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的离心率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{\sqrt{41}}$ |
3.下列函数中既是奇函数又是增函数的是( )
| A. | y=3x+1 | B. | y=2-x-2x | C. | y=x2+1 | D. | y=x|x| |
20.在△ABC中,a,b,c分别为角A,B,C所对的边,且ccosA=b,则△ABC是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 斜三角形 |
7.若不等式x2-ax+a≤1有解,则a的取值范围为( )
| A. | a<2 | B. | a=2 | C. | a>2 | D. | a∈R |
4.芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10kg)与上市时间t(单位:天)的数据情况如下表:
(1)根据上表数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a•bt,Q=alogbt,并说明理由;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
| t | 50 | 110 | 250 |
| Q | 150 | 108 | 150 |
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
5.已知f(x)是R上的奇函数,且当x∈(-∞,0]时,f(x)=-xlg(2m-x+$\frac{1}{2}$).当x>0时,不等式f(x)<0恒成立,则m的取值范围是( )
| A. | (-∞,-1) | B. | (-1,1] | C. | [0,+∞) | D. | [-1,+∞) |