题目内容
5．在平面直角坐标系xoy中，已知△ABC的顶点A（-5，0），C（5，0），顶点B在椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{11}$=1，则$\frac{sinA+sinC}{sinB}$=$\frac{6}{5}$．分析 首先根据所给的椭圆的方程写出椭圆的长轴的长，两个焦点之间的距离，根据正弦定理得到角的正弦值之比就等于边长之比，把边长代入，得到比值．
解答 解：椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{11}$=1的a=6，c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{36-11}$=5，
△ABC的顶点A（-5，0），C（5，0），即为椭圆的两焦点，
由椭圆定义可得，AB+CB=2a=12，
又AC=10，
由正弦定理知$\frac{sinA+sinC}{sinB}$=$\frac{BC+AB}{AC}$=$\frac{12}{10}$=$\frac{6}{5}$，
故答案为：$\frac{6}{5}$．
点评 本题考查椭圆的性质和正弦定理的应用，解题的关键是把角的正弦值之比写成边长之比，进而和椭圆的参数结合起来，需注意特殊点的“巧合”．
练习册系列答案
相关题目
16．已知椭圆$\frac{x^2}{9}+\frac{y^2}{b^2}=1$（0＜b＜3），左、右焦点分别为F1、F2，过F1的直线交椭圆于 A，B两点，若|AF2|+|BF2|的最大值为8，则椭圆的离心率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
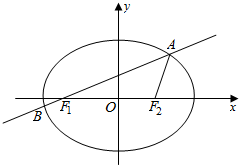如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，F1、F2为其左、右焦点，过F1的直线l交椭圆于A、B两点，△F1AF2的周长为$2（\sqrt{2}+1）$．